Home
Class 12
PHYSICS
A disc of radius R is placed on a square...

A disc of radius R is placed on a square plate of edge 4R made up of the same sheet with their planes parallel such that any two adjacent sides ofsquare touch the disc. Find the distance of the centre of mass of the system from the centre of square plate?

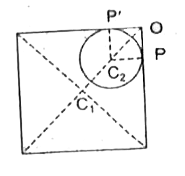
Text Solution

Verified by Experts

Let us consider that `sigma` = mass / area of the sheet
Mass of disc `= m_(1) = pi R^(2) sigma` & mass of square plate `= 16 R^(2)sigma`
By geometry OP. = OP = R
`C_(1)C_(2)=2sqrt(2)R-sqrt(2)R=sqrt(2)R`
`therefore X_(cm)=(sqrt(2)Rxx pi R^(2)sigma + 0 xx 16 R^(2)sigma)/((16+pi)R^(2)sigma)=(sqrt(2)pi R)/(16+pi)` along
`C_(1)C_(2)` from `C_(1)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • COLLISION

    FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE) MATRIX MATCH TYPE|2 Videos

  • COLLISION

    FIITJEE|Exercise Exercise|20 Videos

  • COLLISION

    FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE) COMPREHENSION - II|2 Videos

  • AC CIRCUITS

    FIITJEE|Exercise ASSERTION REASONING TYPE|1 Videos

  • CURRENT ELECTRICITY

    FIITJEE|Exercise Comprehension -4|3 Videos

Similar Questions

Explore conceptually related problems

Centre of mass of the system lies inside disc or square plate and why ?

Four point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

Knowledge Check

  • From a circular disc of radius R , a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is -

    A
    `(4R)/(3(pi-2))`
    B
    `(2R)/(3(pi-2))`
    C
    `(5R)/(7(pi-2))`
    D
    `(R)/(3(pi-1))`

  • Figure shows a square plate of uniform thickness and side length sqrt 2 m . One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is

    A
    `1//3m`
    B
    `1//2m`
    C
    `1//6 m`
    D
    `1//8m`

  • In the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :

    A
    `(4R)/(3pi)`
    B
    `(2r)/(3pi)`
    C
    `sqrt(2)(4R)/(3pi)`
    D
    `sqrt(2)(2R)/(3pi)`

    • Similar Questions

    Explore conceptually related problems

    A solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.

    A uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to L . Locate the position of centre of mass of the system w.r.t. the centre of the square.

    A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.

    A uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.

    In the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6pi at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :

    Home
    Profile