Home
Class 12
PHYSICS
A block of mass M with a semi circular t...

A block of mass M with a semi circular track of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the top point A. The cylinder slips on the semicurcular frictionless track. How far has the block moved when the cylinder reaches the bottom of the track ? How fast is the block moving when the cylinder reaches the bottom of the track ?

Text Solution

Verified by Experts

The correct Answer is:
`(m)/(m+M)(R-r) ; sqrt((2g(R-r))/(M(m+M)))`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • COLLISION

    FIITJEE|Exercise ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I|45 Videos

  • COLLISION

    FIITJEE|Exercise ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)|2 Videos

  • COLLISION

    FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Numerical)|8 Videos

  • AC CIRCUITS

    FIITJEE|Exercise ASSERTION REASONING TYPE|1 Videos

  • CURRENT ELECTRICITY

    FIITJEE|Exercise Comprehension -4|3 Videos

Similar Questions

Explore conceptually related problems

A block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?

A block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?

Knowledge Check

  • A block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g =10ms^(-2))

    A
    `sqrt((10)/(3))ms^(-1)`
    B
    `sqrt((4)/(3))ms^(-1)`
    C
    `sqrt((5)/(2))ms^(-1)`
    D
    `sqrt(10)ms^(-1)`

  • A solid cylinder of radius 0.35 m is released from rest from a height of 1.8 m and rolls down the incline as shown in the figure. What is the angular speed of the cylinder when it reaches the horizontal surface?

    A
    8.2 rad/s
    B
    34 rad/s
    C
    14 rad/s
    D
    67 rad/s

  • A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination theta with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is

    A
    `(3)/(4)(Mgsintheta)/(k)`
    B
    `(2Mgsintheta)/(k)`
    C
    `(Mgsintheta)/(k)`
    D
    none of these

    • Similar Questions

    Explore conceptually related problems

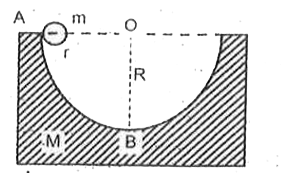
    A block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A . Find the velocity of sphere and track , when the sphere reaches B .

    Figure shows a block A of mass 6 m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.

    A cylinder is released from rest from the top of an incline of inclination theta and length. If the cylinder rolls without slipping. What will be its speed whenit reaches the bottom?

    A uniform solid cylinder of mass 2 kg and radius 0.2 m is released from rest at the top of a semicircular track of radius 0.7 m cut in a block of mass M = 3 kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions: The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is

    A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R. What is the magnitude of the normal force exerted on the block by the hoop when the block has reached the bottom ?

    Home
    Profile