Text Solution
Verified by Experts
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
FIITJEE|Exercise Assignment Problems (Objective) (Level-I)|39 VideosSIMPLE HARMONIC MOTION
FIITJEE|Exercise Assignment Problems (Objective) (Level-I) (Assertion Reasoning type)|3 VideosSIMPLE HARMONIC MOTION
FIITJEE|Exercise Assignment Problems (Subjective) (Level)|20 VideosSEMICONDUCTOR AND DEVICE
FIITJEE|Exercise SOLVED PROBLEMS Objective: Level-I|20 VideosTEST PAPERS
FIITJEE|Exercise PHYSICS|747 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-SIMPLE HARMONIC MOTION-Assignment Problems (Subjective) (Level-II & III)
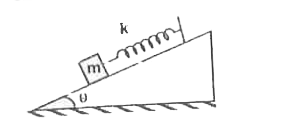
- A block of mass m can slide along a frictionless inclined plane, is at...
Text Solution
|
- Consider a situation shown in the figure. Show that if the blocks are ...
Text Solution
|
- Consider a block symmetrically attached to two identical massless spri...
Text Solution
|
- A disk of mass m is connected to two springs of stiffness k(1) and k(2...
Text Solution
|
- A uniform bar with mass m lies symmetrically across two rapidly rotati...
Text Solution
|
- A rod of length L, cross sectional area A and density rho is hanging f...
Text Solution
|
- A straight rod of light L and mass m is pivoted freely from a point of...
Text Solution
|
- Find the angular frequency of small oscillation of block m in the arra...
Text Solution
|
- A block of mass 'm' is attached to a spring and is placed on a platfor...
Text Solution
|
- Three particles of same mass m are fixed to a uniform circular hoop of...
Text Solution
|
- A uniform semicircular ring of mass m and radius r is hinged at end A ...
Text Solution
|
- In the shown figure mass of the pulley is m and radius 2R. A light con...
Text Solution
|
- The pulley shown in figure has a moment of inertias I about its xis an...
Text Solution
|