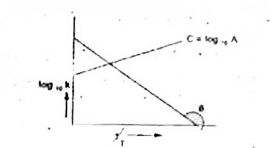
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CHEMICAL KINETICS AND RADIOACTIVITY
FIITJEE|Exercise Matching list type question|3 VideosView PlaylistCHEMICAL KINETICS AND RADIOACTIVITY
FIITJEE|Exercise Matching type single correct|3 VideosView PlaylistCHEMICAL KINETICS AND RADIOACTIVITY
FIITJEE|Exercise Assignment problems (Objective) Level-II (Comprehension-IV)|2 VideosView PlaylistCHEMICAL EQUILIBRIUM
FIITJEE|Exercise MATCHING TYPE QUESTIONS|3 VideosView PlaylistCHEMISTRY IN EVERY DAY LIFE
FIITJEE|Exercise ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II (Numerical Based Questions)|5 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
FIITJEE-CHEMICAL KINETICS AND RADIOACTIVITY-Assignment problems (Objective) Level-II (Comprehension-V)
- When the temperature is increased, heat is supplied which increases th...
Text Solution
|
Play - When the temperature is increased, heat is supplied which increases th...
Text Solution
|
Play - When the temperature is increased, heat is supplied which increases th...
Text Solution
|
Play - When the temperature is increased, heat is supplied which increases th...
Text Solution
|
Play - When the temperature is increased, heat is supplied which increases th...
Text Solution
|
Playing Now