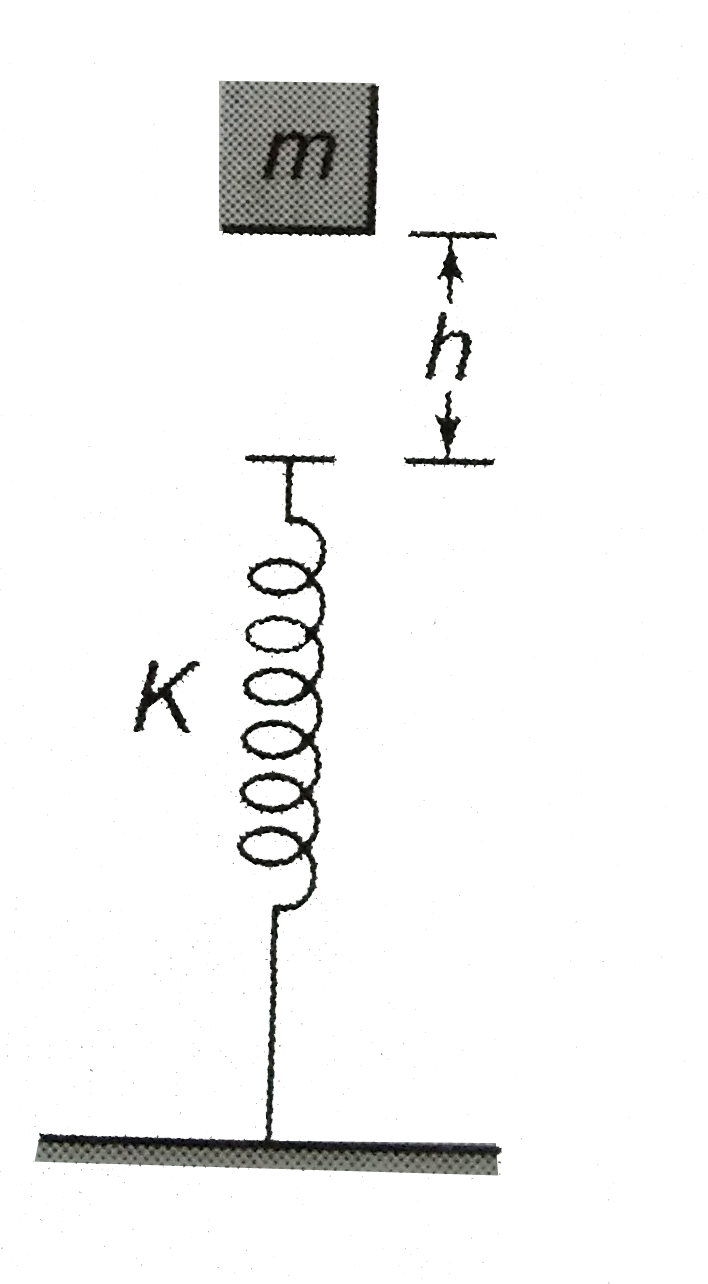Text Solution
Verified by Experts
Topper's Solved these Questions
WORK, ENERGY AND POWER
MODERN PUBLICATION|Exercise NCERT FILE (NCERT Textbook Exercise)|23 VideosWORK, ENERGY AND POWER
MODERN PUBLICATION|Exercise NCERT FILE (NCERT Additional Exercise)|7 VideosWORK, ENERGY AND POWER
MODERN PUBLICATION|Exercise Conceptual Questions|20 VideosWAVES
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|14 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-WORK, ENERGY AND POWER -Tough & Tricky (PROBLEMS)
- A block is released from height h, find the maximum compression of spr...
Text Solution
|
- A smooth hemisphere is kept fixed on a horizontal floor . A small ...
Text Solution
|
- Bob of the simple pendulum is at rest at its lowest position , Sh...
Text Solution
|
- A pendulum bob is given an intial velocity v at this bottom most ...
Text Solution
|
- The bob of a stationary pendulum is given a sharp hit to impart it a h...
Text Solution
|
- Pendulum bob of mass m connected to a string of length l is made ...
Text Solution
|
- Bob of the pendulum is at its bottom most point when it is given hor...
Text Solution
|
- Bob of mass m of the simple pendulum of lngth l is made to go aroun...
Text Solution
|
- A small ball is projected with a velocity u at some angle with ho...
Text Solution
|
- A ball of mass m is moving with a velocity v and it suffers head - on...
Text Solution
|
- A ball strikes a smooth horizontal floor at an angle alpha with the n...
Text Solution
|
- A ball is projected from a point on a smooth horizontal floor at an ...
Text Solution
|
- A ball starts falling freely from a height h from a point on the incli...
Text Solution
|
- A ball of mass 0.1 kg collides head on with another identical ball...
Text Solution
|
- A smooth wedge of mass M is kept at rest on a smooth horizontal su...
Text Solution
|