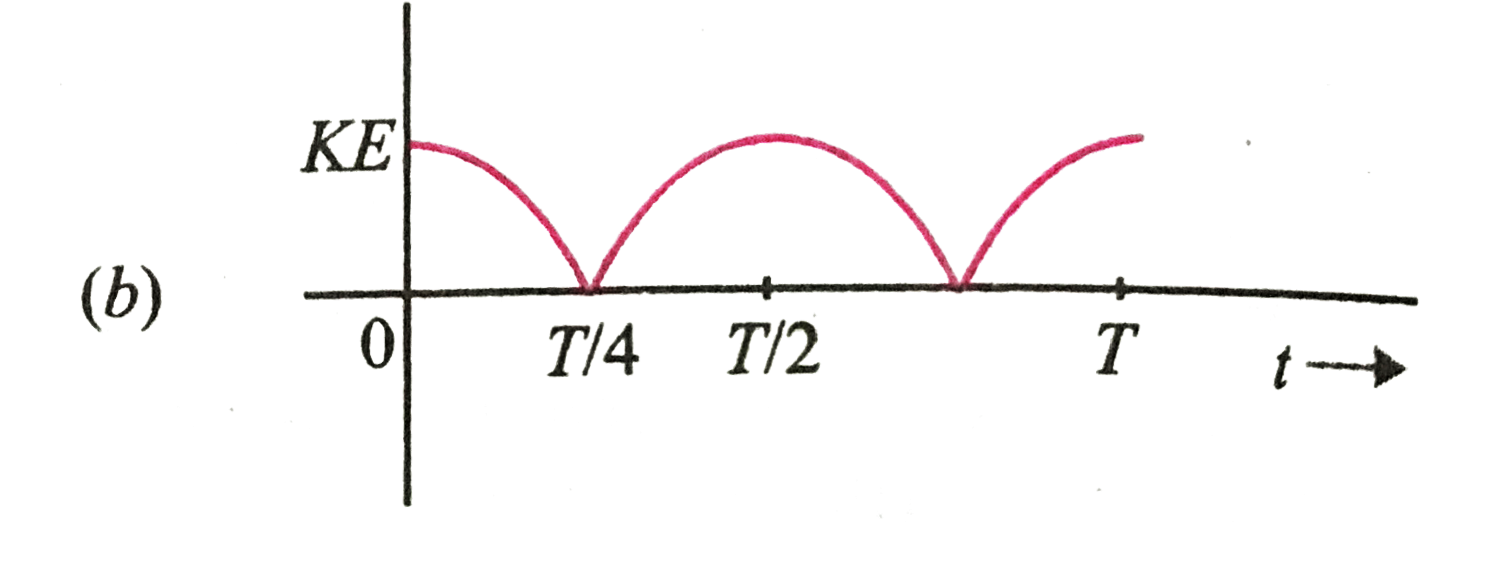
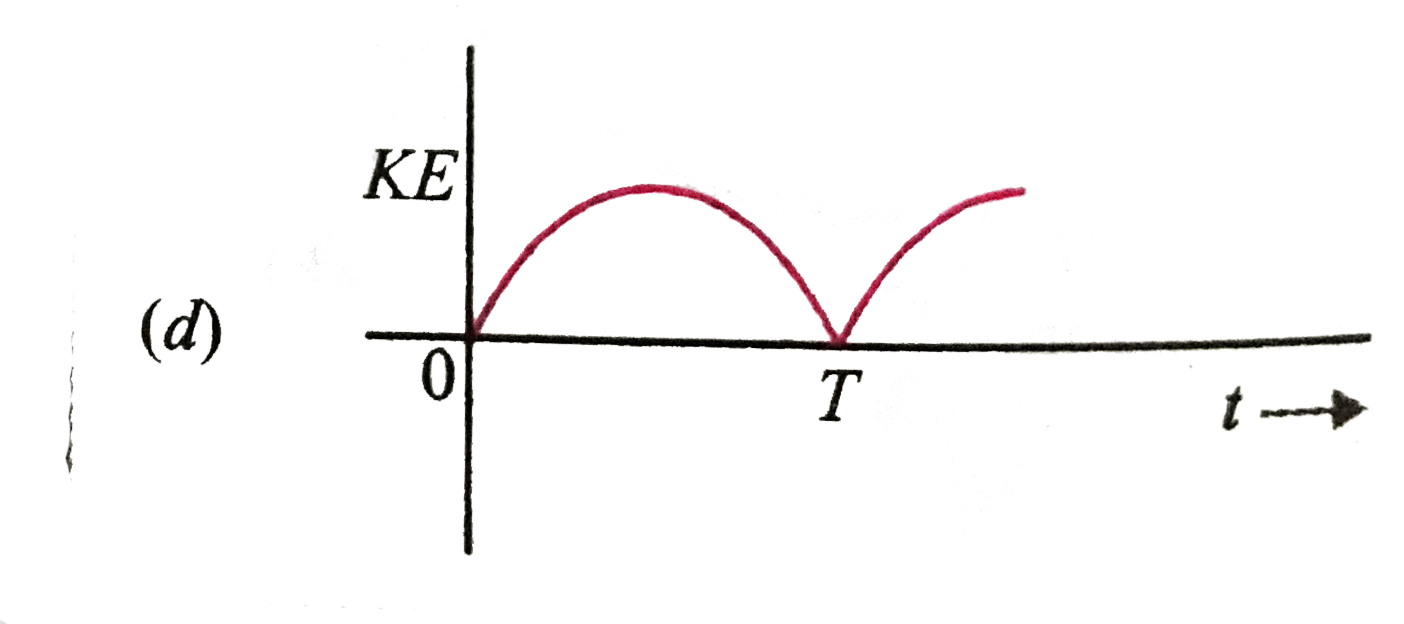
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
RACE
ALLEN|Exercise Basic Maths (Oscillations) (Simple pendulum and types of SHM)|17 VideosView PlaylistRACE
ALLEN|Exercise Basic Maths (Wave Motion & Dopplers Effect) (Fundamental)|23 VideosView PlaylistRACE
ALLEN|Exercise Basic Maths (Dscillations) (Kinematics of SHM)|20 VideosView PlaylistNEWTONS LAWS OF MOTION
ALLEN|Exercise EXERCISE-III|28 VideosView PlaylistSIMPLE HARMONIC MOTION
ALLEN|Exercise Example|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
ALLEN-RACE-Basic Maths (Oscillations) (Energy & spring pendulum)
- If particle is excuting simple harmonic motion with time period T, the...
02:22
|
Playing Now - A particle of mass 4kg moves simple harmonically such that its PE (U) ...
01:44
|
Play - When a mass m attached to a spring it oscillates with period 4s. When ...
01:17
|
Play - Assertion:- A spring of force constatn k is cut in to two piece having...
06:42
|
Play - A linear harmonic oscillator of force constant 2 xx 10^(6)N//m and amp...
01:05
|
Play - A particle moving on x - axis has potential energy U = 2 - 20x + 5x^(2...
03:24
|
Play - The potential energy of a particle executing SHM change from maximum t...
00:43
|
Play - A particle of mass m performs SHM along a straight line with frequency...
03:21
|
Play - Which of the following is correct about a SHM, along a straight line?
02:33
|
Play - Two identical spring of constant K are connected in series and paralle...
03:32
|
Play - A force of 6.4 N stretches a vertical spring by 0.1m. Find the mass th...
01:38
|
Play - Four massless springs whose force constants are 2k, 2k, k and 2k respe...
02:41
|
Play - A system is shown in the figure. The time period for small oscillation...
02:34
|
Play - In a horizontal spring - mass system mass m is released after being d...
02:35
|
Play - A mass M is suspended from a light spring. An additional mass m added ...
03:15
|
Play - A smooth inclined plane having angle of inclination 30^(@) with horizo...
01:35
|
Play