"Whiplash injury" commonly occurs in a rear-end collision where a front car is hit from behind by a second car. In the 1970s, researches concluded that the injury was due to the occupant's head being whipped back over the top of the seat as the car was slammed forward. As a result of this finding, head restraints were built into cars, yet neck injuries in rarend collisions continued to occur.
In a recent test to study neck injury in rear-end collisions, a volunteer was strapped to a seat that was then moves abruptly to simulate a collision by a rear car moving at 10.5 km/h. Figure 2-15 a gives the accelerations of the volunteer's torso and head during the collision, which began at time `t=0`. The torso acceleration was delayed by 40 ms because during that time interval the seat back had to compress against hte volunteer. The head acceleration was delayed by an aditional 70 ms. What was the torso when the head began to accelerate ?

Explanation

KEY IDEA
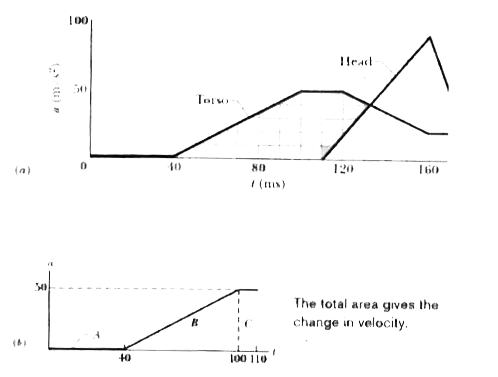
We can calculate the torso speed at any time by finding an area on the torso a(t) graph.
Calculations : We know that the initial torso speed is `v_(0)=0` at time `t_(0)=0` , at the start of the " collision." We want the torso speed `v_(1)` at time `t_(1)=110ms`, which is when the head begins to accelerate.
Combining Eqs. 2-27 and 2-28, we can write
`v_(1)-v_(0)= `( area between acceleration curve and time axis, from `t_(0)` to `t_(1)` ). (2-31)
For convenience, let us separate the area into three regions ( Fig. 2-15b). From 0 to 40 ms, region A has no area :
`"area"_(A)=0`.
From 40 ms to 100 ms, region B has the shape of a triangle, with area
`"area"_(B)= 1/2 (0.060 s) (50 m//s^(2))= 1.5 m//s.`
From 100 ms to 110 ms, region C has the shape of a rectangle, with area
`"area"_(C)= (0.010 s) (50 m//s^(2))= 0.50 m//s`.
Substituting these values and `v_(0)=0` into Eq. 2-31 gives us
`v_(1)-0 = 0+1.5 m//s + 0.50 m//s`,
or `v_(1) = 2.0 m//s = 7.2 km//h`.
Reasoning: When the head is just starting to move forward, the torso already has a speed of 7.2 km/h.
Researchers argue that it is this difference in speeds during the early stage of a rear-end collision that injures the neck. The backward whipping of hte head happens later and could, especially if there is no head restraint, increase the injury.