Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT TELUGU-AREAS -EXERCISE 11.2
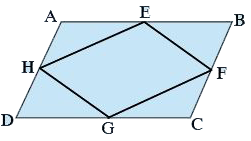
- If E, F G and H are respectively the midpoints of the sides AB, BC, C...
Text Solution
|
- What type of quadrilateral do you get, if you join DeltaAPM, DeltaDPO,...
Text Solution
|
- P and Q are any two points lying on the sides DC and AD respectively o...
Text Solution
|
- P is a point in the interior of a parallelogram ABCD. Show that (i) ...
Text Solution
|
- In the figure, x=…………….cm.
Text Solution
|
- PQRS and ABRS are parallelograms and X is any point on the side BR. Sh...
Text Solution
|
- A farmer has a field in the form of a parallelogram PQRS as shown in t...
Text Solution
|
- Prove that the area of a rhombus is equal to half of the product of th...
Text Solution
|