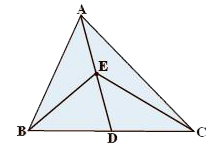
In a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar `DeltaABE = ar DeltaACE`
(ii) `ar DeltaABE=1/4ar(DeltaABC)`

If E be the mid-point of the median AD of DeltaABC , then prove that DeltaBED=1/4DeltaABC .

In the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that (i) BDEF is a parallelogram (ii) ar(DeltaDEF)=1/4ar(DeltaABC) (iii) ar(BDEF)=1/2ar(DeltaABC)

P is a point in the interior of a parallelogram ABCD. Show that (i) ar (DeltaAPB) +ar (DeltaPCD)=1/2ar (ABCD) (ii) ar(DeltaAPD)+ar (DeltaPBC)=ar(DeltaAPB)+ar(DeltaPCD) (Hint : Throught , P draw a line parallel to AB)

Two sides AB, BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of DeltaPQR . Show that: (i) DeltaABM ~= DeltaPQN (ii) DeltaABC ~= DeltaPQR

In the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that (i) ar (DeltaACB) = ar (DeltaACF) (ii) ar (AEDF) = ar (ABCDE)

E is the mid-point of AD , a median of the Delta ABC . The extended BE intersects AC at F. prove that AF=(1)/(3)AC.

In the figure D, E are points on the sides AB and AC respectively of DeltaABC such that ar(DeltaDBC) = ar(DeltaEBC) . Prove that DE || BC.

PQRS and ABRS are parallelograms and X is any point on the side BR. Show that (i) ar(PQRS) = ar(ABRS) (ii) ar(DeltaAXS) =1/2 ar(PQRS)

ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that (i) DeltaABD ~= DeltaACE (ii) AB = AC i.e., ABC is an isosceles triangle.

In right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that : (i) DeltaAMC ~= DeltaBMD (ii) /_DBC is a right angle (iii) Delta DBC ~= DeltaACB (iv) CM = 1/2 AB .