Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-SIMILAR TRIANGLES -OPTIONAL EXERCISE
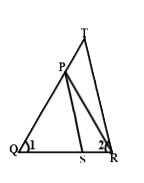
- In the given figure, (QT)/(PR) = (QR)/(QS) and angle 1 = angle 2 ...
Text Solution
|
- Ravi is 1.82m tall. He wants to find the height of a tree in his back...
Text Solution
|
- The diagonal AC of a parallelogram ABCD intersects DP at the point Q, ...
Text Solution
|
- Delta ABC and Delta AMP are two right triangles right angled at B and ...
Text Solution
|
- An aeroplane leaves an airport and flies due north at a speed of 1000 ...
Text Solution
|
- In a right triangle ABC right angled at C, P and Q are points on sides...
Text Solution
|