Home
Class 11
PHYSICS
Find the distance travelled by the parti...

Find the distance travelled by the particle during the time t = 0 to t = 3 second from the figure .

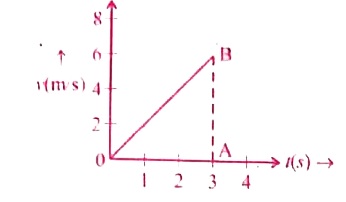
Text Solution

Verified by Experts

(a) `60 m, 6 ms^(-1)` , (b) `36 m, 9 ms^(-1)`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A STRAIGHT LINE

    NCERT TAMIL|Exercise EXERCISES|23 Videos

  • MOTION IN A PLANE

    NCERT TAMIL|Exercise EXCERCISES|32 Videos

  • MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES

    NCERT TAMIL|Exercise EXERCISE (V. NUMERICAL PROBLEMS) |6 Videos

Similar Questions

Explore conceptually related problems

From the velocity time plot shown in figure find the distance travelled by the particle dureing the first 40 seconds. Also find the average velocity during this period.

Figure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.

The distance travelled by a particle in time t is given by s=(2.5m/s^2)t^2 . Find a. the average speed of the particle during the time 0 to 5.0 s, and b. the instantaneous speed at t=5.0 is

From the veloicty time graph of a particle given in figure describe the motion of the particle qualitively int eh interval 0 to 4s. Find a. the distance travelled during first two seconds, b. during the time 2s to 4s, c. during the time 0 to 4s d. displacement during 0 to 4 s. e. acceleration at t=1/2 and f. acceleration at t=2s .

The velocity of a particle is given by the equation, v = 2t^(2) + 5 cms^(-1) . Find the change in velocity of the particle during the time interval between t_(1) = 2s and t_(2) = 4s .

A particle moves along a line according to the law s(t)=2t^(3)-9t^(2)+12t-4 , where tge0 . Find the total distance travelled by the particle in the first 4 seconds.