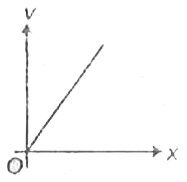
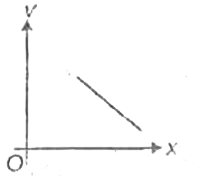
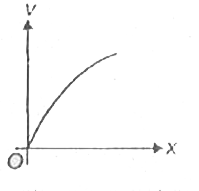
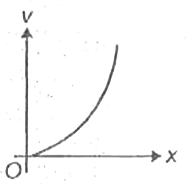
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
Heat & Thermodynamics
NDA PREVIOUS YEARS|Exercise Physics|64 VideosView PlaylistMODERN PHYSICS
NDA PREVIOUS YEARS|Exercise MCQ|42 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NDA PREVIOUS YEARS-Mechanics-Physics
- If some object is weighed when submerged in water, what will happen to...
02:48
|
Play - Which one of the following statements about energy is correct?
01:18
|
Play - If an object moves with constant velocity then which one of the follow...
04:24
|
Play - An object is moving with uniform acceleration a. Its initial velocity ...
01:45
|
Playing Now - Which one of the following has maximum inertia?
02:05
|
Play - Which one of the following statements about gravitational force is NOT...
04:12
|
Play - Whether an object will float or sink in a liquid, depends on
04:06
|
Play - Which one of the following statements about the mass of a body is corr...
03:46
|
Play - A ball balanced on a vertical rod is an example of
03:14
|
Play - Which of the following statements about a fluid at rest in a cup is/ar...
05:10
|
Play - A planet has a mass M(1) and radius R(1). The value of acceleration- d...
04:28
|
Play - Consider the following velocity and time graph: Which one of the ...
Text Solution
|
Play - A ball is released from rest and rolls down an inclined plane, as show...
04:51
|
Play - The coefficient of a real expansion of a material is 1.6xx10^(-5)K^(-1...
03:13
|
Play - Which one of the following energy is stored in the links between the a...
04:27
|
Play - The correct sequence of energy transfer that occurs when an apple fall...
04:11
|
Play - Which one of the following forces is non-central and non- conservative...
06:59
|
Play - Suppose there are two planets, 1 and 2, having the same density but th...
05:21
|
Play - 1 dyne (a unit of force in CGS system) equals to
02:59
|
Play - In the given velocity (V) versus time (t) graph, accelerated and decel...
03:27
|
Play