Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
AREAS RELATED TO CIRCLES
VK GLOBAL PUBLICATION|Exercise Proficiency Exercise (Long Answer Questions)|19 VideosView PlaylistARITHMETIC PROGRESSIONS
VK GLOBAL PUBLICATION|Exercise SELF ASSESSMENT TEST|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
VK GLOBAL PUBLICATION-AREAS RELATED TO CIRCLES-Self -Assessment Test
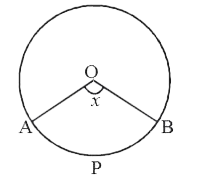
- In fig., O is the centre of a circle. The area of sector OAPB is (5)/(...
03:08
|
Playing Now - The diameter of a circle whose area is equal to the sum of the areas o...
02:07
|
Play - If circumferences of two circles are equal, then what is the ratio bet...
01:28
|
Play - If the perimeter of a circle is numerically equal to its area, find th...
00:43
|
Play - Find the area of a circle whose circumference is 22 cm.
01:40
|
Play - The circumference of a circle exceeds the diameter by 16.8 cm. Find...
02:21
|
Play - The wheels of a car are of diameter 80 cm each. How many complete r...
04:13
|
Play - Find the ratio of the area of the semicircle formed on the diagonal of...
03:45
|
Play - In Fig., two concentric circles with centre O, have radi 21cm and 42cm...
03:24
|
Play - A chord AB of a circle of radius 10 cm makes a right angle at the cent...
04:00
|
Play - The cost of fencing a circular field at the rate Rs 24 per metre is...
01:49
|
Play