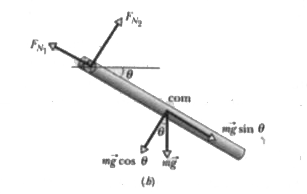
Text Solution
Verified by Experts
|
Topper's Solved these Questions
RIGID BODY DYNAMICS - I
RESNICK AND HALLIDAY|Exercise CHECKPOINT|18 VideosView PlaylistRIGID BODY DYNAMICS - I
RESNICK AND HALLIDAY|Exercise PROBLEMS|100 VideosView PlaylistRELATIVITY
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|5 VideosView PlaylistRIGID BODY DYNAMICS-II
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (Integer Type)|2 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
RESNICK AND HALLIDAY-RIGID BODY DYNAMICS - I-PRACTICE QUESTIONS (INTEGER TYPE))
- A uniform rod of length l and mass M pivoted about its end as shown in...
18:45
|
Playing Now - Four solid sphereas each of diameter sqrt(5) cm and mass 0.5 kg are pl...
02:36
|
Play - A point mass is tied to one end of a cord whose other end passes throu...
03:49
|
Play - Two small bals A and B, each of mass m, are joined rigidlyl by a light...
03:16
|
Play