Home
Class 11
PHYSICS
An air chamber of volume V has a neck ar...

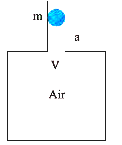
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

Text Solution

Verified by Experts

`T=2pisqrt((Vm)/(Ba^(2)))` where B is the bulk modulus of air. For isothermal changes B=P.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • OSCILLATIONS

    NCERT GUJARATI|Exercise Exercises|28 Videos

  • MOTION IN A STRAIGHT LINE

    NCERT GUJARATI|Exercise ADDITIONAL EXERCISES|5 Videos

  • PHYSICAL WORLD

    NCERT GUJARATI|Exercise EXERCISES|8 Videos

Similar Questions

Explore conceptually related problems

A rectangular pipe having cross-sectional area A is closed at one end and at its other end a block having same cross-section is placed so that the system is airtight. In the equilibrium position of the block, the pressure and volume of air enclosed in the pipe and P and V respectively. Prove that the block performs SHM when it is given a small displacement 'x' inward and released. Also find the period of this SHM. Assume the walls to be frictionless and compression of air to be isothermal.

An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M . The piston and the cylinder have equal cross-sectional area A . When the piston is in equilibrium, the volume of the gas is V_(0) and its pressure is P_(0) . The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency

A potato gun first a potato horizontally down a half-open cylinder of cross-sectional area A . When the gun is fired , the potato slug is at rest , the volume betweeen the end of the cylinder and the potato is V_(0) , and the pressure of the gas in this volume is P_(0) . The atmospheric pressure is P_("atm") . where P__(0) gt P_("atm") . The gas in the cylinder is diatomic, this means that C_(V) = (5R)/(2) and C_(P) = (7R)/(2) . The potato moves down the cylinder quickly enough that no heat is transferred to the gas. Friction between the potato and the barreel is negligible and no gas leaks around the potato . The parameters P_(0) , P_("atm"), V_(0) and A are fixed, but the overall length L of the barrel may be varied. The maximum kinetic energy E_("max") with which the potato can exit the barrel?

When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, F_(w)=6pietarv . in this formula eta in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=etaAv//z . For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P_(2)-P_(1) . The flow rate of expressed by the formula Q=(piR^(4)(P_(2)-P_(1)))/(8etaL) poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula R_(e)=(2overline(v)rhoR)/(eta) In which overline(v) is the average speed rho is the density eta is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be rho=1000kg//m^(3) Q. Blood vessel is 0.10 m in length and has a radius of 1.5xx10^(-2) m blood flows at rate of 10^(-7)m^(3)//s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?

When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, F_(w)=6pietarv . in this formula eta in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=etaAv//z . For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P_(2)-P_(1) . The flow rate of expressed by the formula Q=(piR^(4)(P_(2)-P_(1)))/(8etaL) poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula R_(e)=(2overline(v)rhoR)/(eta) In which overline(v) is the average speed rho is the density eta is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be rho=1000kg//m^(3) Q. If the sphere in previous question has mass of 1xx10^(-5)kg what is its terminal velocity when falling through water? (eta=1xx10^(-3)Pa-s)

When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, F_(w)=6pietarv . in this formula eta in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=etaAv//z . For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P_(2)-P_(1) . The flow rate of expressed by the formula Q=(piR^(4)(P_(2)-P_(1)))/(8etaL) poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula R_(e)=(2overline(v)rhoR)/(eta) In which overline(v) is the average speed rho is the density eta is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be rho=1000kg//m^(3) Q. What is the viscous force on a glass sphere of radius r=1mm falling through water (eta=1xx10^(-3)Pa-s) when the sphere has speed of 3m/s?

When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, F_(w)=6pietarv . in this formula eta in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=etaAv//z . For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P_(2)-P_(1) . The flow rate of expressed by the formula Q=(piR^(4)(P_(2)-P_(1)))/(8etaL) poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula R_(e)=(2overline(v)rhoR)/(eta) In which overline(v) is the average speed rho is the density eta is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be rho=1000kg//m^(3) Q. Calculate the highest average speed that blood (rho~~1000kg//m^(3) ) could have and still remain in laminar flow when it flows through the arorta (R=8xx10^(-3)m ) Take the coeffiicient of viscosity of blood to be 4xx10^(-3)Pa-s

When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, F_(w)=6pietarv . in this formula eta in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=etaAv//z . For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P_(2)-P_(1) . The flow rate of expressed by the formula Q=(piR^(4)(P_(2)-P_(1)))/(8etaL) poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula R_(e)=(2overline(v)rhoR)/(eta) In which overline(v) is the average speed rho is the density eta is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be rho=1000kg//m^(3) Q. Which of the following may be concluded from the information in the passage?

Home
Profile