Text Solution
Verified by Experts
|
Topper's Solved these Questions
XII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SET I|70 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SET II|9 VideosView PlaylistSAMPLE PAPER 2019
XII BOARDS PREVIOUS YEAR|Exercise SECTION D|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-XII BOARDS-SECTION - B
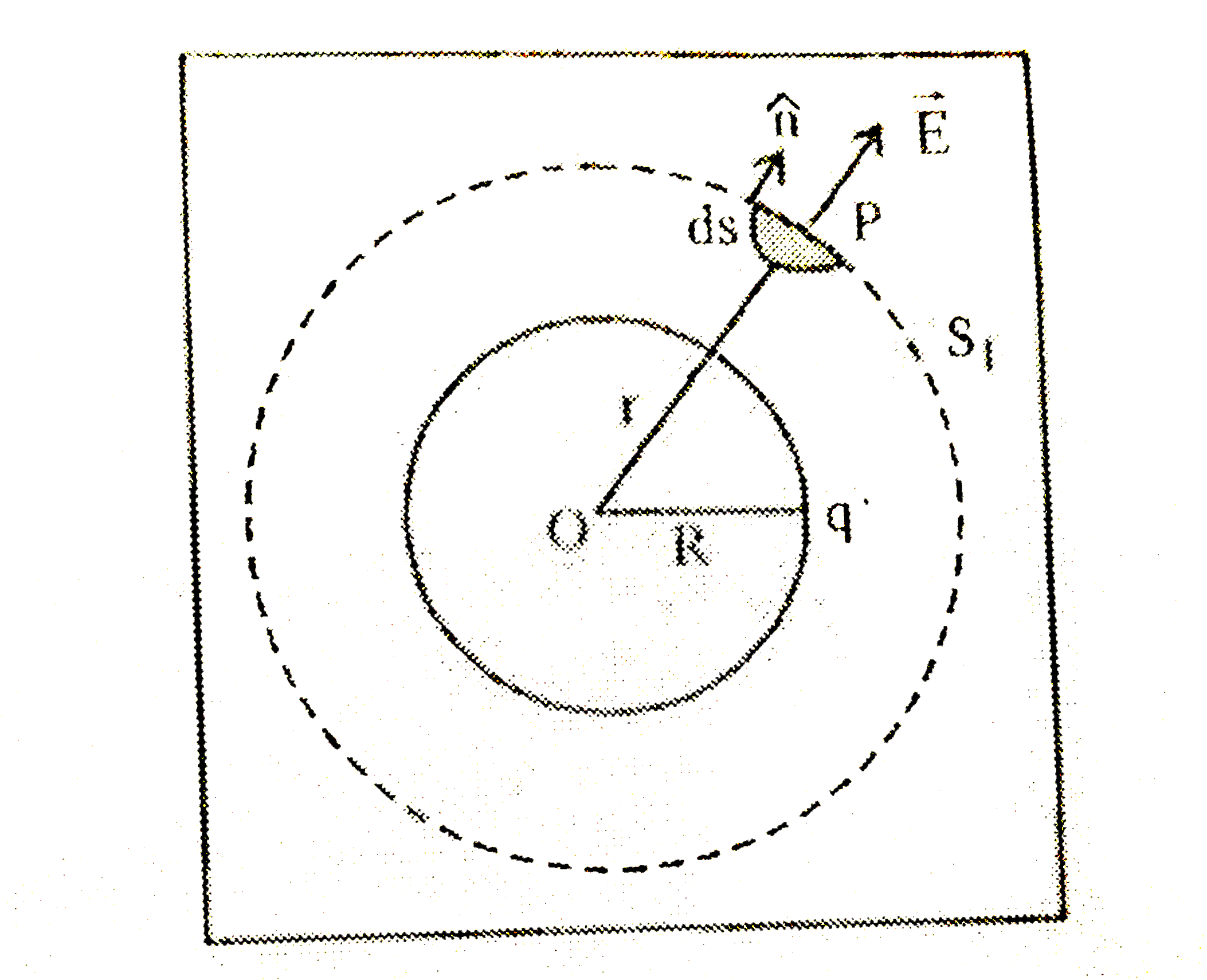
- (a) Using Gauss's law, derive an expression for the electric field in...
09:01
|
Playing Now - Using Gauss's law obtain the expression for the electric field due to ...
07:31
|
Play - Two large parallel plane sheets have uniform charge densities + sigma ...
02:38
|
Play - A long straight wire AB carries a current of 4 A. A proton P travels a...
02:39
|
Play - A capacitor, made of two parallel plates each of plate area A and sepa...
03:56
|
Play - A beam of light converges at a point P. Now a convex lens is placed in...
01:31
|
Play - An object is kept in front of a concave mirror of focal length 15 cm. ...
03:27
|
Play - Explain giving reason, how the resolving power of a compound microscop...
02:58
|
Play - The figure shows a modified Young's double slit experimental set-up. ...
03:25
|
Play - A certain n-p-n transistor has the common emitter output characteristi...
02:20
|
Play