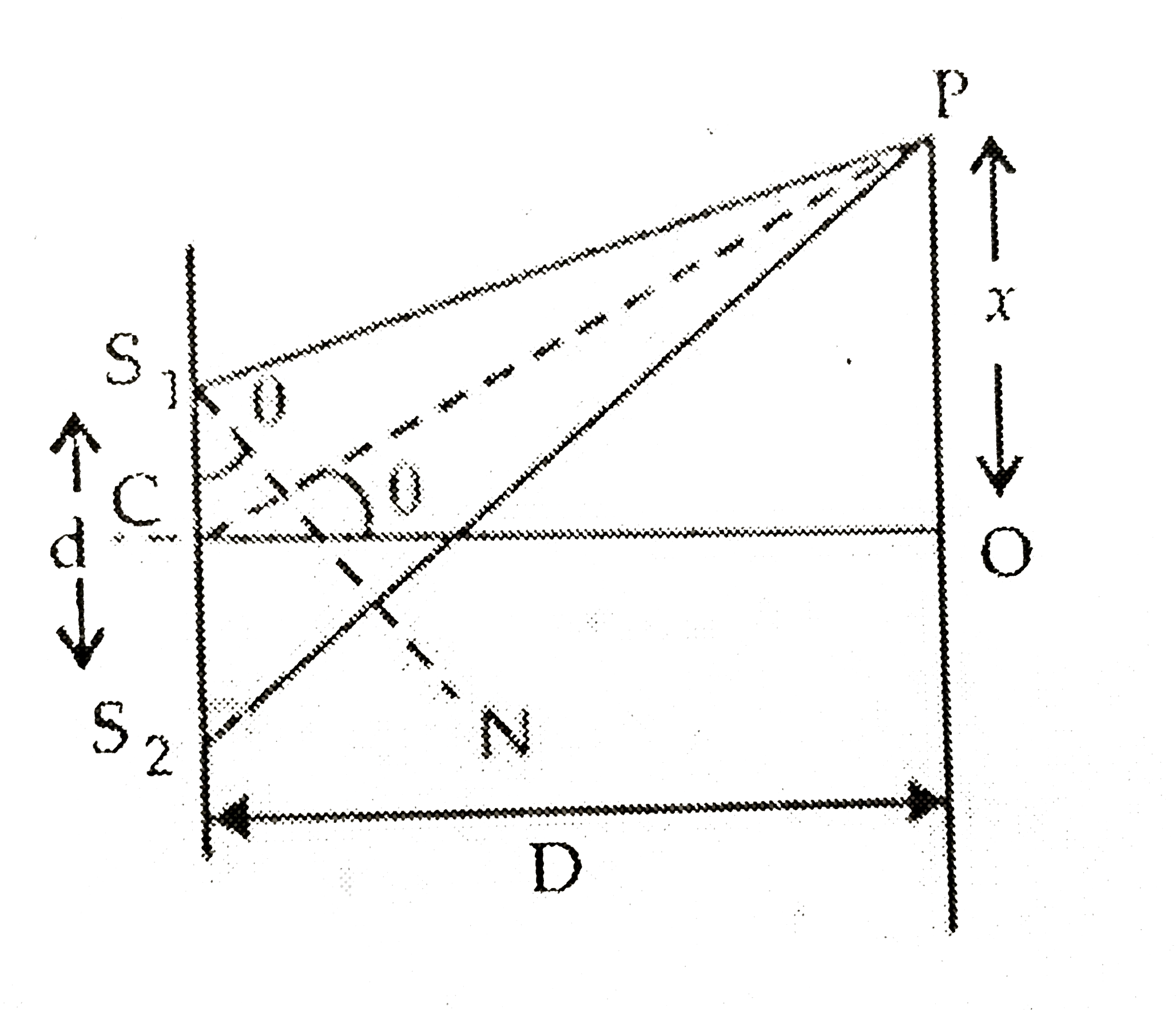
Text Solution
Verified by Experts
|
Topper's Solved these Questions
XII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise PHYSICS (Theory) [SET - II]|6 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise PHYSICS (Theory) [SET - III]|10 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise [Set-III]|6 VideosView PlaylistSAMPLE PAPER 2019
XII BOARDS PREVIOUS YEAR|Exercise SECTION D|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-XII BOARDS-PHYSICS (Theory) [SET - I]
- Explain the scattering of light with an example.
Text Solution
|
Play - Describe briefly with the help of a circuit diagram, how the flow of c...
Text Solution
|
Play - In the given block diagram of a receiver, Figure, identify the boxes l...
02:18
|
Play - A light bulb is rated 100 W for 220 V ac supply of 50 Hz. Calculate ...
00:57
|
Play - An alternating voltage given by V = 140 sin 314 t is connected across ...
02:31
|
Play - A circular coil of N turns and radius R carries a current I. It is unw...
03:21
|
Play - Deduce the expression for the electrostatic energy stored in a capacit...
05:57
|
Play - Calculate the value of the resistance R in the circuit shown in the fi...
04:49
|
Play - You are given three lenses L(1),L(2) and L(3) each of focal length 20 ...
05:12
|
Play - Explain thermionic emission, field emission and photoelectric emission...
Text Solution
|
Play - Obtain the resonant frequency (omega(r)) of a series LCR circuit withL...
01:45
|
Play - Mention three different modes of propagation used in communications sy...
02:22
|
Play - Draw a plot of potential energy of a pair of nucleons as a function of...
Text Solution
|
Play - In a Geiger- Marsden experiment, calculate the distance of closest app...
03:25
|
Play - The ground state energy of hydrogen atom is -13.6eV. If an electron ma...
03:59
|
Play - Define relaxation time of the free electrons drifting in conductor. Ho...
Text Solution
|
Play - (a) In Young's double slit experiment, derive the condition for (i) co...
10:27
|
Playing Now - (a) How does an unpolarized light incident on polaroid get polarized ?...
02:28
|
Play - (a) Write the expression for the force, vecF, acting on a charged part...
Text Solution
|
Play - (a) Explain, giving reasons, the basic difference in converting galvan...
Text Solution
|
Play