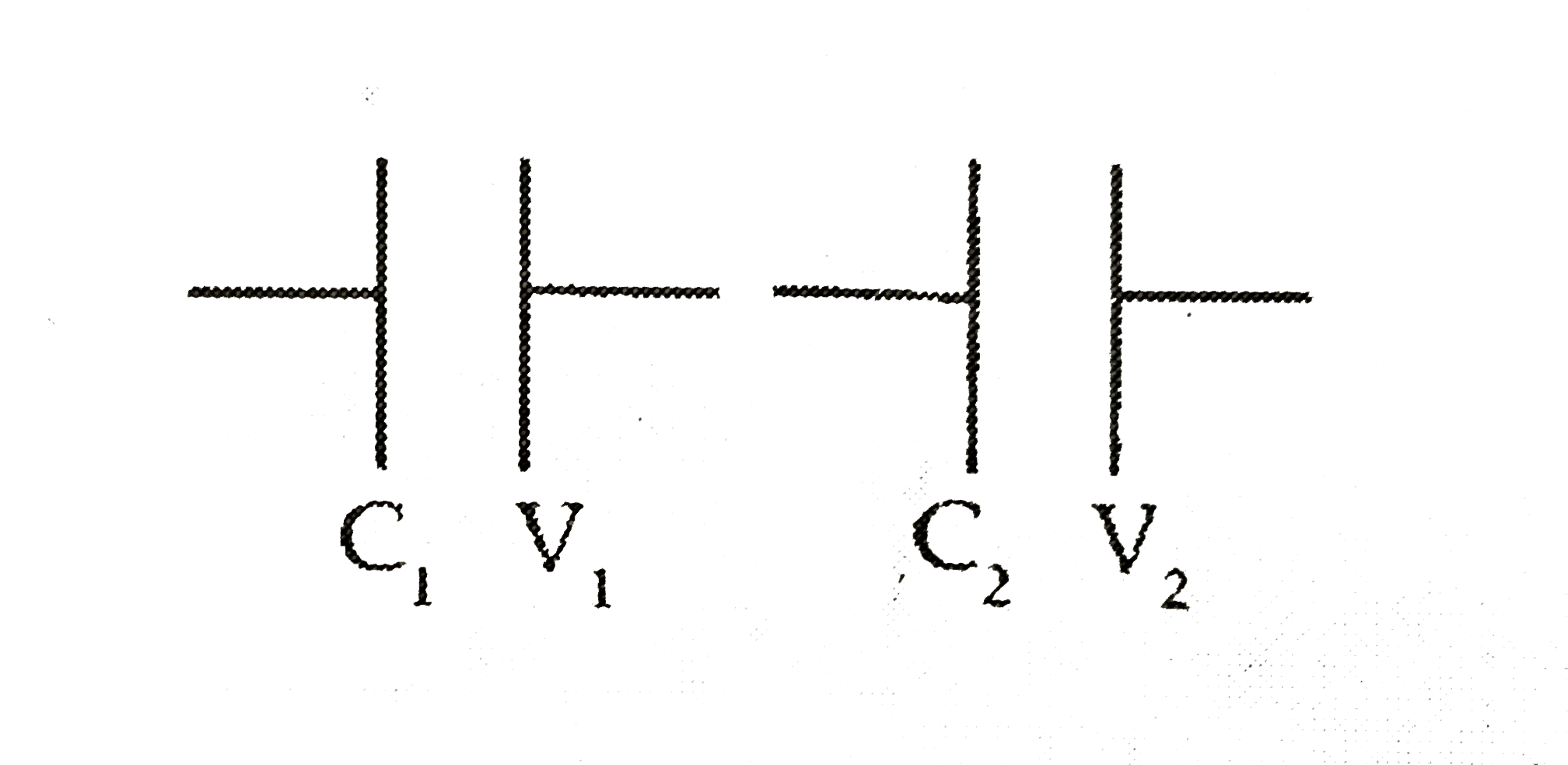Text Solution
Verified by Experts
|
Topper's Solved these Questions
XII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SECTION - C|13 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SECTION - A|7 VideosView PlaylistXII BOARDS
XII BOARDS PREVIOUS YEAR|Exercise SECTION - D|6 VideosView PlaylistSAMPLE PAPER 2019
XII BOARDS PREVIOUS YEAR|Exercise SECTION D|6 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-XII BOARDS-SECTION - E
- (a) Explain with the help of suitable diagram , the two processes whic...
Text Solution
|
Play - (a) Describe briefly three factors which justify the need for modula...
Text Solution
|
Play - Two point charges q and - q are located at points (0 , 0 , - a ) and ...
08:36
|
Play - A capacitor of capacitance C(1) is charged to a potential V(1) while ...
06:36
|
Playing Now - (a) Draw graphs showing the variations of inductive reactnace and cap...
Text Solution
|
Play - State the principle of working of a transformer. (b) Define effi...
04:04
|
Play