Text Solution
Verified by Experts
|
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
U-LIKE SERIES|Exercise LONG ANSWER QUESTIONS-II|11 VideosView PlaylistMOVING CHARGES AND MAGNETISM
U-LIKE SERIES|Exercise SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)|5 VideosView PlaylistMOVING CHARGES AND MAGNETISM
U-LIKE SERIES|Exercise SHORT ANSWER QUESTIONS|41 VideosView PlaylistMODEL TEST PAPER 3 (UNSOLVED)
U-LIKE SERIES|Exercise SECTION A|3 VideosView PlaylistNUCLEI
U-LIKE SERIES|Exercise Self Assessment Test|10 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
U-LIKE SERIES-MOVING CHARGES AND MAGNETISM -LONG ANSWER QUESTIONS-I
- Write using Biot-Savart law, the expression for the magnetic field vec...
Text Solution
|
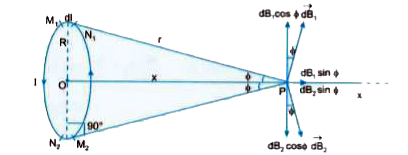
Playing Now - State Biot- Savart law. Use to obtain the magnetic field at a point du...
Text Solution
|
Play - A long solenoid of length 'l' having carries a current I. Deduce the e...
Text Solution
|
Play - Using Ampere's circuital law, obtain an expression for the magnetic fi...
Text Solution
|
Play - What does a toroid consist of ? Show that for an ideal toroid of close...
Text Solution
|
Play - An iron ring of relative permeability mur, has windings of insulated c...
Text Solution
|
Play - A long straight wire of a circular cross-section (radius r) carries a ...
Text Solution
|
Play - Consider the motion of a charged particle of mass m and charge q movin...
Text Solution
|
Play - Deduce an expression for the frequency of revolution of a charged part...
Text Solution
|
Play - A uniform magnetic field vecB is set up along the positive x-axis. A p...
Text Solution
|
Play - (a) Write the expression for the force vecF acting on a particle of ma...
Text Solution
|
Play - (i) Obtian the expression for the cyclotron frequency. (ii) A deuter...
Text Solution
|
Play - Derive an expression for the force acting on a current carrying conduc...
Text Solution
|
Play - Write the expression for the force vecF acting on a charged particle o...
Text Solution
|
Play - Two long straight parallel current conductors are kept at a distance d...
Text Solution
|
Play - A rectangle loop of size l xx b carrying a steady current I is placed ...
Text Solution
|
Play - Two small identical circular loops, marked (1) and (2), carrying equal...
Text Solution
|
Play - A circular coil of 200 turns and radius 10 cm is placed in a uniform m...
Text Solution
|
Play - A rectangular loop of wire of size 4 cm xx 10 cm carries a steady curr...
Text Solution
|
Play - A wire AB is carrying current of 12 A and is lying on the table. Anoth...
Text Solution
|
Play