Home
Class 10
MATHS
In a Delta ABC, XY || BC and XY = 1/2 BC...

In a `Delta ABC`, `XY || BC` and `XY = 1/2 BC`. If the area of `Delta AXY = 10 cm^(2)`. Find the area of trapezium XYCB.

Text Solution

Verified by Experts

The correct Answer is:
`30 cm^(2)`
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    OSWAAL PUBLICATION|Exercise TOPIC-3 AREA OF SIMILAR TRIANGLES (MULTIPLE CHOICE QUESTIONS)|10 Videos

  • TRIANGLES

    OSWAAL PUBLICATION|Exercise TOPIC-3 AREA OF SIMILAR TRIANGLES (VERY SHORT ANSWER TYPE QUESTIONS)|6 Videos

  • TRIANGLES

    OSWAAL PUBLICATION|Exercise TOPIC-1 BASIC PROPORTIONALITY THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)|17 Videos

  • SURFACE AREA AND VOLUMES

    OSWAAL PUBLICATION|Exercise EXERCISE 15.5|5 Videos

Similar Questions

Explore conceptually related problems

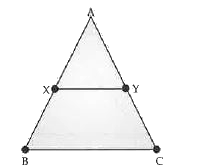
In DeltaABC , XY || BC and XY=(1)/(2)BC . If the area of DeltaAXY=10cm^(2) , find the area of trapezium XYCB.

In the trapezium ABCD, AB || CD , AB = 2 CD and ar(Delta AOB) = 84 cm^(2) , find the area of Delta COD .

If Delta ABC ~ Delta DEF, BC = 3cm, EF = 4cm, and Area of Delta ABC = 54 cm^(2) , then Area of Delta DEF is

In Delta ABC , XY || BC , (AY)/(CY) = 1/2 and AX = 4 . Find BX .

AX an BY are perpendiculars to segment XY . If AO = 5 cm , BO = 7 cm and Area of Delta AOX= 150 cm^2 , find the area of Delta BOY .

ABCD is square F is the mid-point of All. BE is one third of BC. If the area of Delta FBE is 108 cm^(2) , Find the length of AC.

In Delta ABC , XY || AC and XY divides the triangle into two parts of equal area. Find the ratio of (AX)/(XB) .

In the figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact are the lengths 4 cm and 3 cm respectively. If the area of DeltaABC=21 cm^(2) , find the length of sides AB and AC.

In DeltaABC, let b=6, c=10and r_(1) =r_(2)+r_(3)+r then find area of Delta ABC.