Home
Class 10
MATHS
AB is a diameter of circle. P is a point...

AB is a diameter of circle. P is a point on the semicircle APB. AH and BK are perpendiculars from A and B respectively to the tangents at P. Prove that `AH+BK=AB`.

Answer

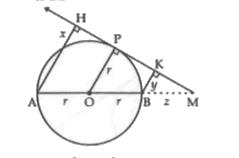
Step by step text solution for AB is a diameter of circle. P is a point on the semicircle APB. AH and BK are perpendiculars from A and B respectively to the tangents at P. Prove that AH+BK=AB. by MATHS experts to help you in doubts & scoring excellent marks in Class 10 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CIRCLES

    ZEN PUBLICATION|Exercise ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS)|2 Videos

  • CIRCLES

    ZEN PUBLICATION|Exercise ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)|9 Videos

  • CIRCLES

    ZEN PUBLICATION|Exercise ZEN ADDITIONAL QUESTIONS ( SHORT ANSWER [SA] TYPE - 2 - QUESTIONS)|13 Videos

  • ARITHMETIC PROGRESSIONS

    ZEN PUBLICATION|Exercise ZEN ADDITIONAL QUESTIONS (HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS)|4 Videos

  • CO-ORDINATE GEOMETRY

    ZEN PUBLICATION|Exercise ZEN ADDITIONAL QUESTIONS - HIGHER ORDER THINKING SKILLS [HOTS] QUESTIONS|14 Videos

Similar Questions

Explore conceptually related problems

AB is a diameter of a circle and C is any point on the circumference of the circle, then :

In figure, bar(AB) is a diameter of the circle, bar(CD) is a chord equal to the radius of the circle. bar(AC) and bar(BD) when extended intersect at a point E. Prove that angle AEB = 60^@ .

If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to

In the figure, O is the centre of the circle and AB = CD. OM is perpendicular on bar(AB) and bar(ON) is perpendicular on bar(CD) . Then prove that OM = ON.

In the given figure, AD is a diameter of a circle with centre O and AB is a tangent at A. C is a point on the circle such that DC produced intersects the tangent at B and |__ABD=50^(@) . Find |__COA .

In a Delta ABC , let P and Q be points on AB and AC respectively such that PQ || BC . Prove that the median AD bisects PQ.

Prove that the tangent at any point of a circle is perpendicular to the radius through the point of tangent

If A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P on AB such that AP = (3)/(7) AB.

In Fig . two chords AB and CD intersect each other at the point P. prove that : AP.PB=CP.DP

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Home
Profile