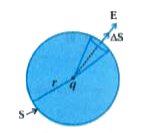
Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION A QUESTIONS- ANSWERS (APPLICATION OF GAUSS.S LAW)|1 VideosELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION A QUESTIONS- ANSWERS (FIELD DUE TO AN INFINITELY LONG STRAIGHT UNIFORMLY CHARGED WIRE)|1 VideosELECTRIC CHARGES AND FIELDS
KUMAR PRAKASHAN|Exercise SECTION A QUESTIONS- ANSWERS (CONTINOUS CHARGE DISTRIBUTION)|4 VideosDUAL NATURE OF RADIATION AND MATTER
KUMAR PRAKASHAN|Exercise Section-D (MCQs asked in GUJCET/Board Exam)|1 VideosELECTROMAGNETIC INDUCTION
KUMAR PRAKASHAN|Exercise Section D MCQs (MCQs asked in Competitive Exams )|38 Videos
Similar Questions
Explore conceptually related problems