Home
Class 12
PHYSICS
A hollow charged conductor has a tiny ho...

A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hold is `(sigma)/(2pi epsilon_(0))hatn` where `hatn` is the unit vector in the outward normal direction, and a is the surface charge density near the hole.

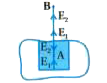
Text Solution

Verified by Experts

As shown in figure, assume that the hole on the conducting surface is filled by conductor. According to Gauss.s law, at A on surface,
`oint vecE.dvecS =q/epsilon_(0)`
`EdS cos0^(@) = (sigmadS)/epsilon_(0) [therefore sigma = q/(ds)]`
`therefore E.dS = (sigmadS)/(epsilon_(0))`
`therefore vecE = sigma/(epsilon_(0)).hatn`
Which is electric field outside the conductor. Above electric field can be written as,
`vecE = vecE_(1) + vecE_(2)`..........(2)
where `vecE_(1)` = electric field at point `P_0` just outside the conductor (adjacent to point P on the surface) due to charge at point P and `vecE_(2)`= electric field at point P (or at `P_0`) flue to remaining charges on the given charged hollow conductor.
When hollow charged conductor does not have any hole at point P on the surface we have `vecE_(1)` and `E_2` pointing along `hatn` and so from equation (2), we can write,
`E = E_(1) + E_(2) = sigma/(epsilon_(0))`...........(3)
Now consider point `P_(p)` , adjacent to point P and just inside the conductor in figure (a), where resultant electric field `vecE` is `vec0`. Hence,
`vecE = vecE_(1) + vecE_(2) = vec0`
`therefore vecE_(1) = - vecE_(2)`
`therefore vecE_(1) = E_(2)` (Taking magnitude).......(4)
From eqn. (3) and (4)
`2E_(2) = sigma/(epsilon_(0))`
`therefore E_(2) = sigma/(2epsilon_(0))`..........(5)
Now, when we have a hole at point P electric field at point P,- in the hole due to remaining charges will be,
`E_(2) = sigma/(2epsilon_(0))hatn`.............(6)
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • ELECTRIC CHARGES AND FIELDS

    KUMAR PRAKASHAN|Exercise SECTION B NUMERICALS (NUMERICAL FOR .DARPAN. BASED ON TEXTBOOK)|8 Videos

  • ELECTRIC CHARGES AND FIELDS

    KUMAR PRAKASHAN|Exercise SECTION C NCERT EXEMPLAR SOLUTION (MULTIPLE CHOICE QUESTIONS (MCQs))|7 Videos

  • ELECTRIC CHARGES AND FIELDS

    KUMAR PRAKASHAN|Exercise SECTION B NUMERICALS (NUMERICAL FROM TEXTUAL EXERCISES)|24 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    KUMAR PRAKASHAN|Exercise Section-D (MCQs asked in GUJCET/Board Exam)|1 Videos

  • ELECTROMAGNETIC INDUCTION

    KUMAR PRAKASHAN|Exercise Section D MCQs (MCQs asked in Competitive Exams )|38 Videos

Similar Questions

Explore conceptually related problems

A hollow charged conductor has a tiny hole cut in to its surface show that the electric field in the hole is n where n is the charge density near the hole

(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by (E_(2)-E_(1)).n = sigma/epsilon_(0) where hatn is a unit vector normal to the surface at a point and sigma is the surface charge density at that point. (The direction of hatn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is sigma hatn //epsilon_(0) . (b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]

Knowledge Check

  • lf the electric field around a surface is given by |vecE|=(Q)/(E_(0)|vecA|) where vecA is the normal area of surface and Q_("in") is the charge enclosed by the surface. This relation of Gauss's law is valid when

    A
    the surface is equipotential.
    B
    the magnitude of the electric field is constant.
    C
    the magnitude of the electric field is constant and the surface is equipotential.
    D
    for all the Gaussian surfaces.

    • Similar Questions

    Explore conceptually related problems

    Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

    What are the forms, of energy into which the electrical energy of the atmosphere is dissipated during a lightning ? (Hint : The earth has an electric field of about 100 Vm^(-1) at its surface In the downward direction, corresponding to a surface charge density = - 10^(-9) cm^(-2) . Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth).

    Answer the following: (a) The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm^(-1) . Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside!) (b) A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1m^(2) . Will he get an electric shock if he touches the metal sheet next morning (c) The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged? (d) What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning? (Hint: The earth has an electric field of about 100 Vm^(-1) at its surface in the downward direction, corresponding to a surface charge density = –10^(–9) Cm^(–2) . Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge onthe earth.)

    Figure shows a uniformly charged hemisphere of radius R. It has a volume charge density rho . If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

    A spherical conductor of radius 12 cm has a charge of 1.6 xx 10^(-7) C distributed uniformly on its surface. What is the electric field (a) inside the sphere (b) just outside the sphere (c) at a point 18 cm from the centre of the sphere?

    A spherical conductor of radius 12 cm has a charge of 1.6 xx 10^(-7) C distributed uniformly on its surface . What is the electric field (a) inside the sphere (b) just outside the sphere. (c) at a point 18 cm from the centre of the sphere ?

    If the uniform surface charge density on the infinite plane sheet is sigma , electric field near the surface will be

    Home
    Profile