Home
Class 9
MATHS
In the given figure, BOC is a diameter o...

In the given figure, `BOC` is a diameter of a circle and `AB =AC` . Then , `/_ ABC = ?`

A

`30^(@)`

B

`45^(@)`

C

`60^(@)`

D

`90^(@)`

Text Solution

Verified by Experts

The correct Answer is:
B
Since an angle in a semicircle is a right angle `/_ BAC = 90^(@)`
`:. /_BAC + /_ ACB = 90^(@)`
Now, `AB= AC implies /_ABC = /_ ACB = 45^(@)`
Promotional Banner

Topper's Solved these Questions

  • CIRCLES

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|5 Videos

  • BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON

    RS AGGARWAL|Exercise EXERCISE 17B|16 Videos

  • CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE

    RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|20 Videos

Similar Questions

Explore conceptually related problems

In the given figure, AB is a diameter of a circle and CD is perpendicular to AB, if AB = 10 cm and AE = 2 cm, then what is the length of ED ?

In the given figure, AB is the diameter of the circle. Find the value of angleACD :

In the given figure,O is the centre of the circle and BA =AC. If /_ABC=50^(@), find /_BOC and /_BDC.

If the given figure, AB is diameter of the circle, C and D lie on the semicircle. angle ABC = 65^(@) and angle CAD = 45^(@) , find angle DCA .

In the given figure,AB=AC. prove that :

In the given figure, AB is the diameter of the circle, angleADC = 120^(@) . Find angleCAB :

In the given figure, /_COB = 40^(@), AB is the diameter of the circle. Find m/_CAB :

In the given figure if AB = AC then find theta .

RS AGGARWAL-CIRCLES -MULTIPLE CHOICE QUESTION(MCQ)
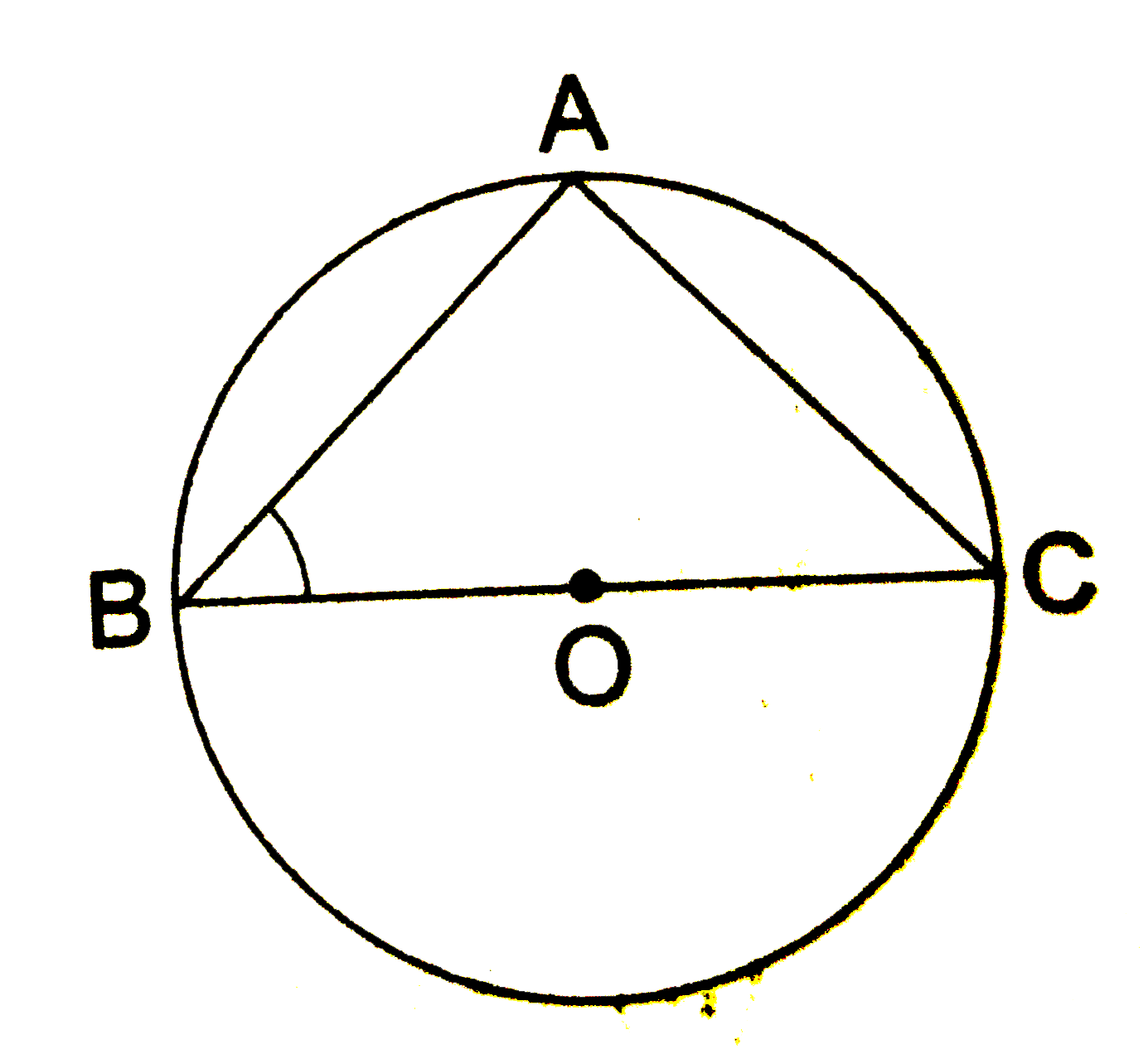
  1. In the given figure, BOC is a diameter of a circle and AB =AC . Then ,...

    Text Solution

    |

  2. In the given figure, O is the centre of a circle and / ACB = 30^(@) ...

    Text Solution

    |

  3. In the given figure, O is the centre of a circle. If angle OAB = 40^(@...

    Text Solution

    |

  4. In the given figure, AOB is a diameter of a circle with centre O such...

    Text Solution

    |

  5. AB and CD are two equal to chord of a circle with centre O such that ...

    Text Solution

    |

  6. In the given figure, CD is the diameter of a circle with centre O and...

    Text Solution

    |

  7. In the given figure, O is the centre of a circle and diameter AB bisec...

    Text Solution

    |

  8. In the given figure, BOC is a diameter of a circle with centre O . If ...

    Text Solution

    |

  9. In the given figure, AB is a chrod of a circle with centre O and AB is...

    Text Solution

    |

  10. In the given figure, AB is a chord of a circle with centre O and BOC i...

    Text Solution

    |

  11. In the given figure, Delta ABC and Delta DBC arre inscribed in a circ...

    Text Solution

    |

  12. In the given figure, BOC is a diameter of a circle with centre O. If /...

    Text Solution

    |

  13. In the given figure, O is the centre of a circle . If / OAC = 50^(@) t...

    Text Solution

    |

  14. In the given figure, O is the centre of a circle in which / OBA = 20^(...

    Text Solution

    |

  15. In the given figure, O is the centre of a circle. If / AOB = 100^(@) a...

    Text Solution

    |

  16. In the given figure, O is the centre of a circle . The, / OAB = ?

    Text Solution

    |

  17. In the given figure, O is the centre of a circle and / AOC = 120^(@) ....

    Text Solution

    |

  18. In the given figure, O is the centre of a circle and / OAB=50^(@). The...

    Text Solution

    |

  19. In the given figure, AB and CD are two intersecting chords of acircle...

    Text Solution

    |

  20. In the given figure, O is the centre of a circle and chords AC and BD ...

    Text Solution

    |