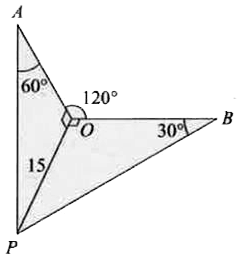
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
HEIGHTS AND DISTANCES
MCGROW HILL PUBLICATION|Exercise SOLVED EXAMPLES (LEVEL 1 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))|30 VideosView PlaylistHEIGHTS AND DISTANCES
MCGROW HILL PUBLICATION|Exercise SOLVED EXAMPLES (LEVEL 2 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))|15 VideosView PlaylistELLIPSE
MCGROW HILL PUBLICATION|Exercise Previous Years B-Architecture Entrance Examination Papers|6 VideosView PlaylistHYPERBOLA
MCGROW HILL PUBLICATION|Exercise QUESTION FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS|8 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
A
B
C
D
Submit
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
MCGROW HILL PUBLICATION-HEIGHTS AND DISTANCES -QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
- Two ships A and B are sailing straight away from the foot of a tower O...
Text Solution
|
Playing Now - A vertical pole stands at a point A on the boundary of a circular park...
Text Solution
|
Play - Two vehicles C(1) and C(2) start from a point P and travel east of P a...
Text Solution
|
Play - An observer standing at a point P on the top of a hill near the sea-sh...
Text Solution
|
Play