A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
GRAVITATION
MCGROW HILL PUBLICATION|Exercise HIGHER ORDER THINKING QUESTIONS|25 VideosView PlaylistELECTRIC CURRENT
MCGROW HILL PUBLICATION|Exercise HIGHER ORDER THINKING QUESTIONS|29 VideosView PlaylistHEAT
MCGROW HILL PUBLICATION|Exercise HIGHER ORDER THINKING QUESTIONS|15 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
MCGROW HILL PUBLICATION-GRAVITATION -HIGHER ORDER THINKING QUESTIONS
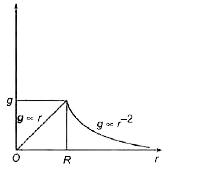
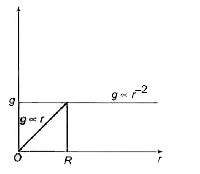
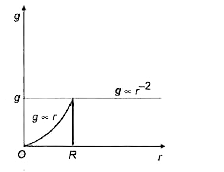
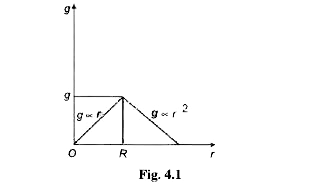
- The variation of g with height or depth (r ) is shown correctly by the...
09:47
|
Playing Now - The weight of a person on earth is 900 N. His weight on the moon will ...
03:27
|
Play - If G is universal gravitational constant and g is acceleration due to ...
01:37
|
Play - Gravity meter is used to measure
Text Solution
|
Play - Two speres of radii r and 2r touching each other the force of attra...
02:18
|
Play - The tidel waves in the sea are primarily due to gravitational effect ...
03:02
|
Play - If the distance between the sun and the earth is increased by three ti...
01:13
|
Play - The ratio between masses of two planets is 2:3 and ratio between their...
03:38
|
Play - If the earth suddenly shrinks (without changing mass) to half of its p...
01:02
|
Play - F(g) and F(e) represent gravitational and electrostatic force respecti...
04:21
|
Play - Two planets have same density but different radii The acceleration du...
04:02
|
Play - Gravitation on moon is (1)/(6) th of that on earth. When a balloon fil...
01:38
|
Play - The accelearation due to gravity on a planet is 1.96 ms^(-2) if tit ...
06:34
|
Play - Which of the following cannot be used for measuring time in a spacesh...
Text Solution
|
Play - If both the mass and radius of the earth, each decreases by 50%, the a...
02:37
|
Play - The line joining the places on earht having same values of g are calle...
Text Solution
|
Play - If different planets have the same density but diferent radii then the...
01:51
|
Play - Rate of change of weight near the earth 's surface varies with height ...
04:41
|
Play - The period of geostationary satellite is
01:05
|
Play - Where will it be profitable to purchase 1 kilogram sugar
01:43
|
Play - As we go from the equator to the poles, the value of g
05:56
|
Play