A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
CIRCLES
NCERT EXEMPLAR ENGLISH|Exercise EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS|10 VideosView PlaylistCIRCLES
NCERT EXEMPLAR ENGLISH|Exercise EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS|10 VideosView PlaylistARITHMETIC PROGRESSIONS
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|10 VideosView PlaylistCONSTRUCTIONS
NCERT EXEMPLAR ENGLISH|Exercise Exercise 10.4 Long Answer type Questions|7 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-CIRCLES-EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
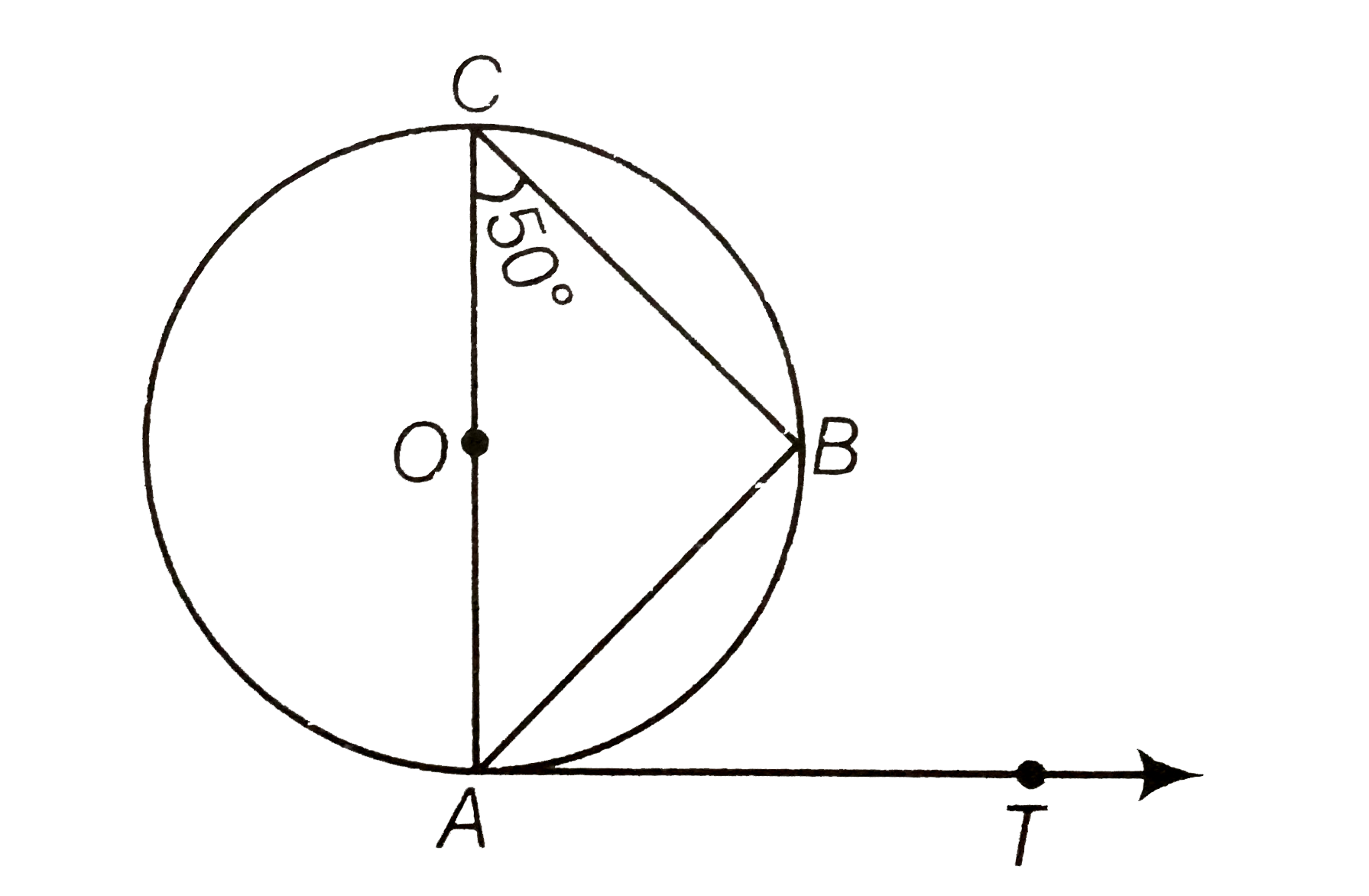
- In figure, AB is a chord of the circle and AOC is its diameter such th...
05:34
|
Playing Now - If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF=BC+...
05:05
|
Play - Let s denotes the semi-perimeter of a DeltaABC in which BC=a, CA=b and...
03:47
|
Play - From an external point P, two tangents, PA and PB are drawn to a circl...
04:20
|
Play - If AB is chord of a circle with centre O, AOC is a diameter and AT is ...
03:41
|
Play - Two circles with centers O and O' of radii 6cm and 8 cm respectively i...
11:33
|
Play - In a right angle triangle Delta ABC is which / B = 90^@ a circle is dr...
08:11
|
Play - In figure, tangents PQ and PR are drawn to a circle such that angleRPQ...
07:23
|
Play - AB is a diameter of a circle and AC is its chord such that angleBAC=30...
07:09
|
Play - . Prove that the tangent drawn at the mid-point of an arc of a circle ...
04:26
|
Play - In a figure the common tangents, AB and CD to two circles with centers...
05:49
|
Play - Type V: O is the center of the circle of radius 5cm. T is a point such...
10:17
|
Play - The tangent at a point C of a circle and a diameter AB when extended i...
06:22
|
Play - If an isosceles triangle A B C in which A B=A C=6c m is inscribed in a...
13:30
|
Play - A is a point at a distance 13 cm from the centre O of a circle of radi...
07:08
|
Play