Home
Class 12
MATHS
(Cosine Formulae) if a ,b ,c are the len...

(Cosine Formulae) if `a ,b ,c` are the lengths of the sides opposite respectively to the angles `A ,B ,C` of a triangle `A B C ,` show that (I) `cosA=(b^2+c^2-a^2)/(2b c)` (ii) `cosB=(c^2+a^2-b^2)/(2a c)` (iii) (i) `cosC=(a^2+b^2-c^2)/(2a b)`

Text Solution

Verified by Experts

Here, components of C are c cos A and c sin A is drawn.

Since, `vec(CD)=b-c cosA`
In `DeltaBDS" "a^(2)=(b-cosA)^(2)+(csinA)^(2)`
`impliesa^(2)=b^(2)+c^(2)cos^(2)A-2bc cosA+c^(2)sin^(2)A`
`implies2bc cosA=b^(2)-a^(2)+c^(2)(cos^(2)Asin^(2)A)`
`:.cosA=(b^(2)+c^(2)-a^(2))/(2ab)`
Promotional Banner

Topper's Solved these Questions

  • VECTOR ALGEBRA

    NCERT EXEMPLAR ENGLISH|Exercise OBJECTIVE TPYE QUESTIONS|27 Videos

  • VECTOR ALGEBRA

    NCERT EXEMPLAR ENGLISH|Exercise OBJECTIVE TPYE QUESTIONS|27 Videos

  • THREE DIMENSIONAL GEOMETRY

    NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPE QUESTIONS|16 Videos

Similar Questions

Explore conceptually related problems

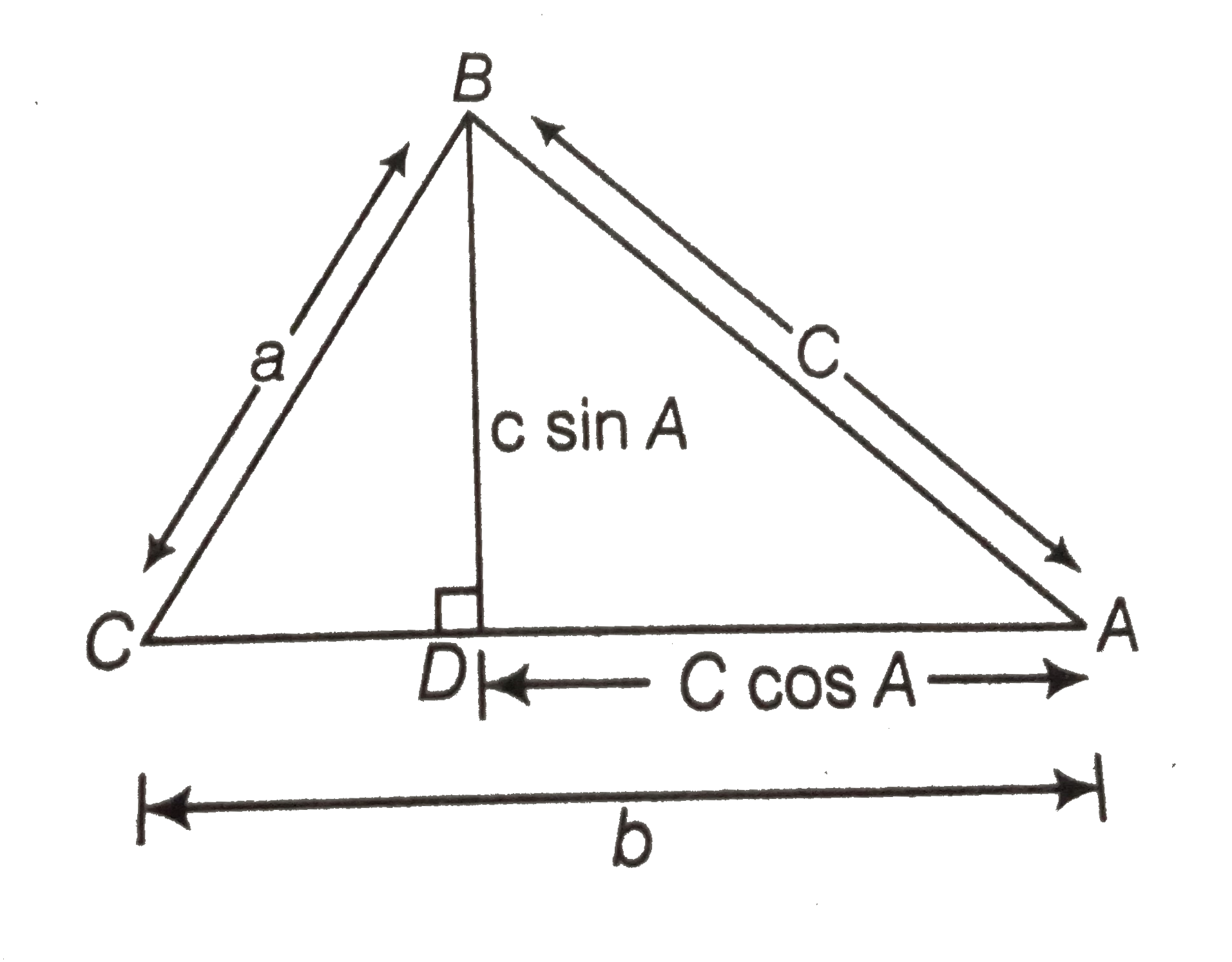
(Cosine Formulae) if a ,b ,c are the lengths of the sides opposite respectively to the angles A ,B ,C of a triangle A B C , show that cosA(b^2+c^2-a^2)/(2b c) (ii) cosB(c^2+a^2-b^2)/(2a c) (iii) (i) cosC(a^2+b^2-c^2)/(2a b)

If any triangle A B C , that: (b^2-c^2)/(cosB+cosC)+(c^2-a^2)/(cosC+cosA)+(a^2-b^2)/(cosA+cosB)=0

In any triangle A B C prove that: sin((B-C)/2)=((b-c)/a)cosA/2

For any triangle ABC, prove that (cosA)/a+(cosB)/b+(cosC)/c=(a^2+b^2+c^2)/(2a b c)

In any triangle A B C , prove that: ("sin"(B-C))/("sin"(B+C))=(b^2-c^2)/(a^2)

In a triangle ABC , acosB + b cosC + c cosA =(a+b+c)/2 then

In any Delta A B C , prove that: a(b\ cos C-c cosB)=b^2-c^2

If A, B and C are interior angles of a triangle ABC, then show that "sin"((B+C)/2)=cosA/2 .

In any Delta A B C , prove that: (cos A)/a+(cos B)/b+(cos C)/c=(a^2+b^2+c^2)/(2a b c)

If A ,\ B ,\ C are the interior angles of a triangle A B C , prove that tan((C+A)/2)=cotB/2 (ii) sin((B+C)/2)=cosA/2