Text Solution
Verified by Experts
The correct Answer is:
|
Topper's Solved these Questions
TRIGONOMETRIC FUNCTIONS
CENGAGE ENGLISH|Exercise Concept Application Exercises 2.5|16 VideosView PlaylistTRIGONOMETRIC FUNCTIONS
CENGAGE ENGLISH|Exercise Concept Application Exercises 2.6|1 VideosView PlaylistTRIGONOMETRIC FUNCTIONS
CENGAGE ENGLISH|Exercise Concept Application Exercises 2.3|4 VideosView PlaylistTRIGONOMETRIC EQUATIONS
CENGAGE ENGLISH|Exercise Archives (Matrix Match Type)|1 VideosView PlaylistTRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
CENGAGE ENGLISH|Exercise Matrix Match Type|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-TRIGONOMETRIC FUNCTIONS -Concept Application Exercises 2.4
- Let (-3, -4) be a point on the terminal side of theta. Find the sine, ...
02:22
|
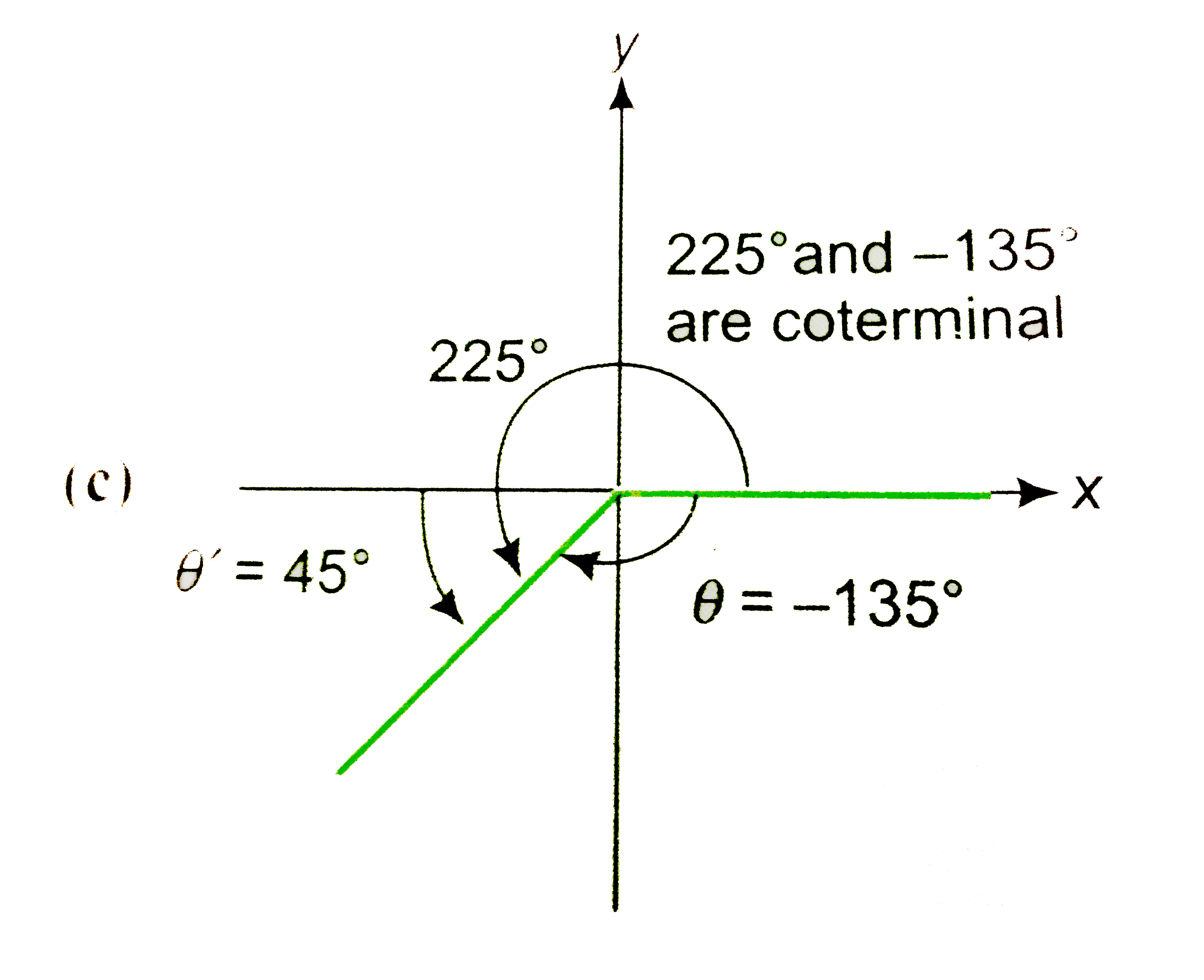
Play - Find the reference angle theta'for the following angles in standerd po...
04:09
|
Playing Now - Evaluate each of the following trigonometric functions: (a) cos.(4...
03:22
|
Play - State if the given pairs of angles are coterminal. (a) -185^@,535^...
03:27
|
Play