Home
Class 9
MATHS
Show that the diagonals of a square a...

Show that the diagonals of a square are equal and bisect each other at right angles.

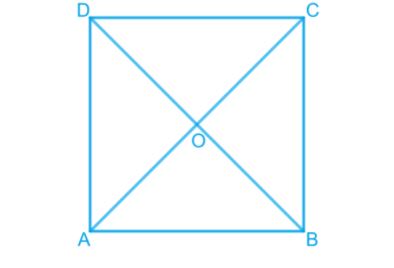
Text Solution

Verified by Experts


Given: The quadrilateral is a square.
To prove: Diagonals of a square are equal and bisect each other at right angles.
Thus, we have to prove` AC = BD, OA = OC, OB = OD`, and `∠AOB = 90^@`
...
Promotional Banner

Topper's Solved these Questions

  • PROBABILITY

    RD SHARMA ENGLISH|Exercise All Questions|67 Videos

  • RATIONALISATION

    RD SHARMA ENGLISH|Exercise All Questions|130 Videos

Similar Questions

Explore conceptually related problems

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Prove that the diagonals of a parallelogram bisect each other.

Prove that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Show that the diagonals of a rhombus are perpendicular to each other

Show that the diagonals of a rhombus are perpendicular to each other

The diagonals of a parallelogram bisect each other.

Show that the diagonals of a rhombus bisect each other at right angles.

RD SHARMA ENGLISH-QUADRILATERALS-All Questions
  1. Show that the diagonals of a rhombus are perpendicular to each othe...

    Text Solution

    |

  2. If the diagonals of a parallelogram are equal and intersect at right ...

    Text Solution

    |

  3. Show that the diagonals of a square are equal and bisect each other...

    Text Solution

    |

  4. The diagonals of a rectangle A B C D meet at Odot If /B O C=44^0, find...

    Text Solution

    |

  5. P Q R S is a square. P R and S Q intersect at Odot State the measure o...

    Text Solution

    |

  6. ABCD is a rectangle in which diagonal AC bisects /A as well as /C ....

    Text Solution

    |

  7. A B C D is a rhombus with /A B C=56^0dot Determine /A C Ddot

    Text Solution

    |

  8. Each of the four angles of a rectangle is a right angle.

    Text Solution

    |

  9. Each of the four sides of a rhombus is of the same length.

    Text Solution

    |

  10. A B ,C D are two parallel lines and a transversal l intersects A B at ...

    Text Solution

    |

  11. If A B C and D E F are two triangles such that A B ,B C are respe...

    Text Solution

    |

  12. In Figure, A B C D is a parallelogram and X\ a n d\ Y are points on th...

    Text Solution

    |

  13. In Figure, A B C is an isosceles triangle in which A B=A Cdot and C P|...

    Text Solution

    |

  14. In Figure, X ,Y are the mid-points of opposite sides A B and D C of a ...

    Text Solution

    |

  15. Two segments A C and B D bisect each other at O . Prove that A B C D i...

    Text Solution

    |

  16. Each of the angles of a square is a right angle and each of the four ...

    Text Solution

    |

  17. The diagonals of a rectangle are of equal length.

    Text Solution

    |

  18. If the diagonals of a quadrilateral bisect each other, then the qua...

    Text Solution

    |

  19. A quadrilateral is parallelogram if its opposite angles are equal.

    Text Solution

    |

  20. A quadrilateral is a parallelogram if its opposite sides are equal.

    Text Solution

    |