A liquid in a beaker has temperature `theta(t)` at time t and `theta_0` is temperature of surroundings, then according to Newton's law of cooling the correct graph between `log_e( theta-theta_0)` and t is :
A liquid in a beaker has temperature `theta(t)` at time t and `theta_0` is temperature of surroundings, then according to Newton's law of cooling the correct graph between `log_e( theta-theta_0)` and t is :
A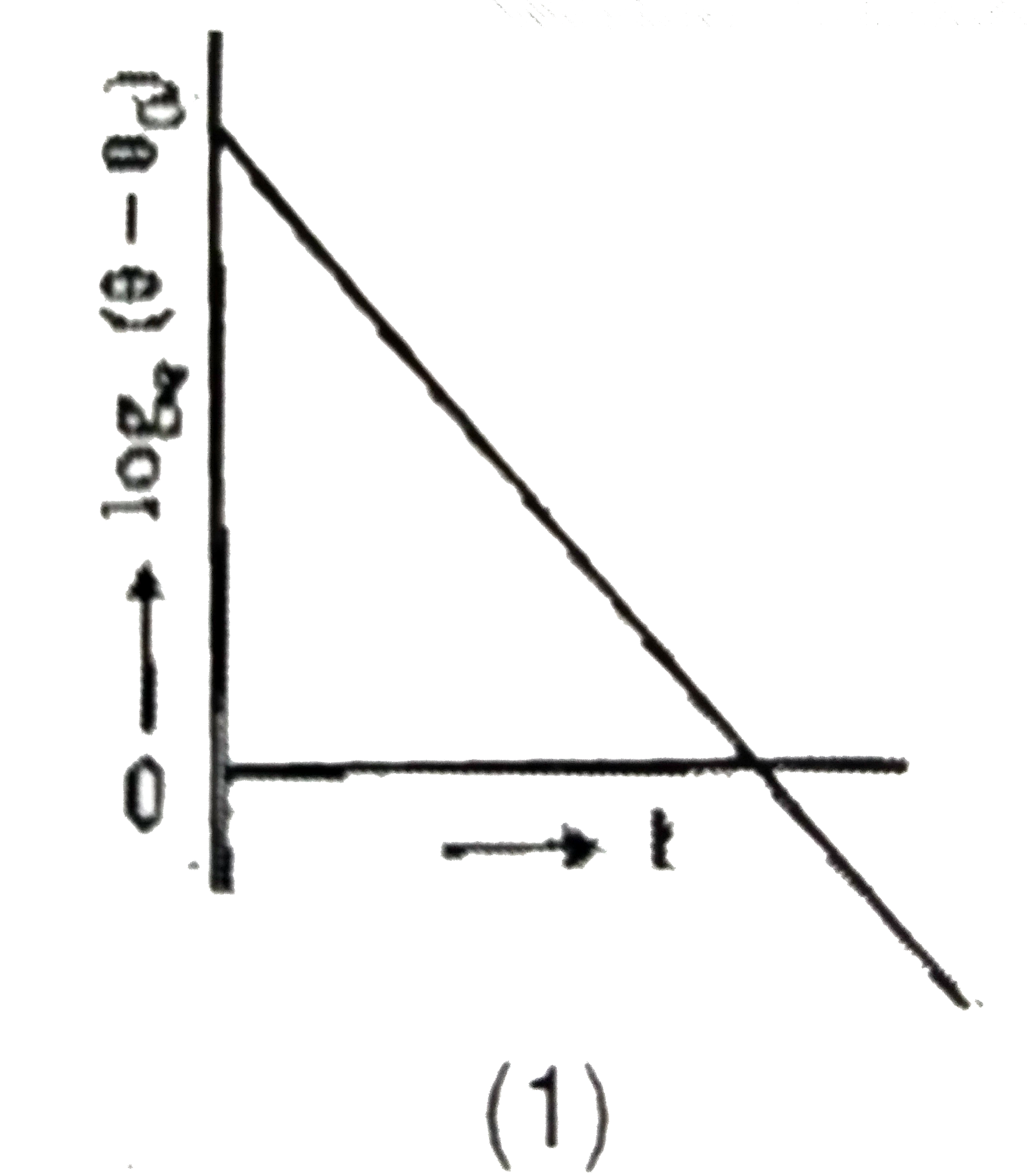

B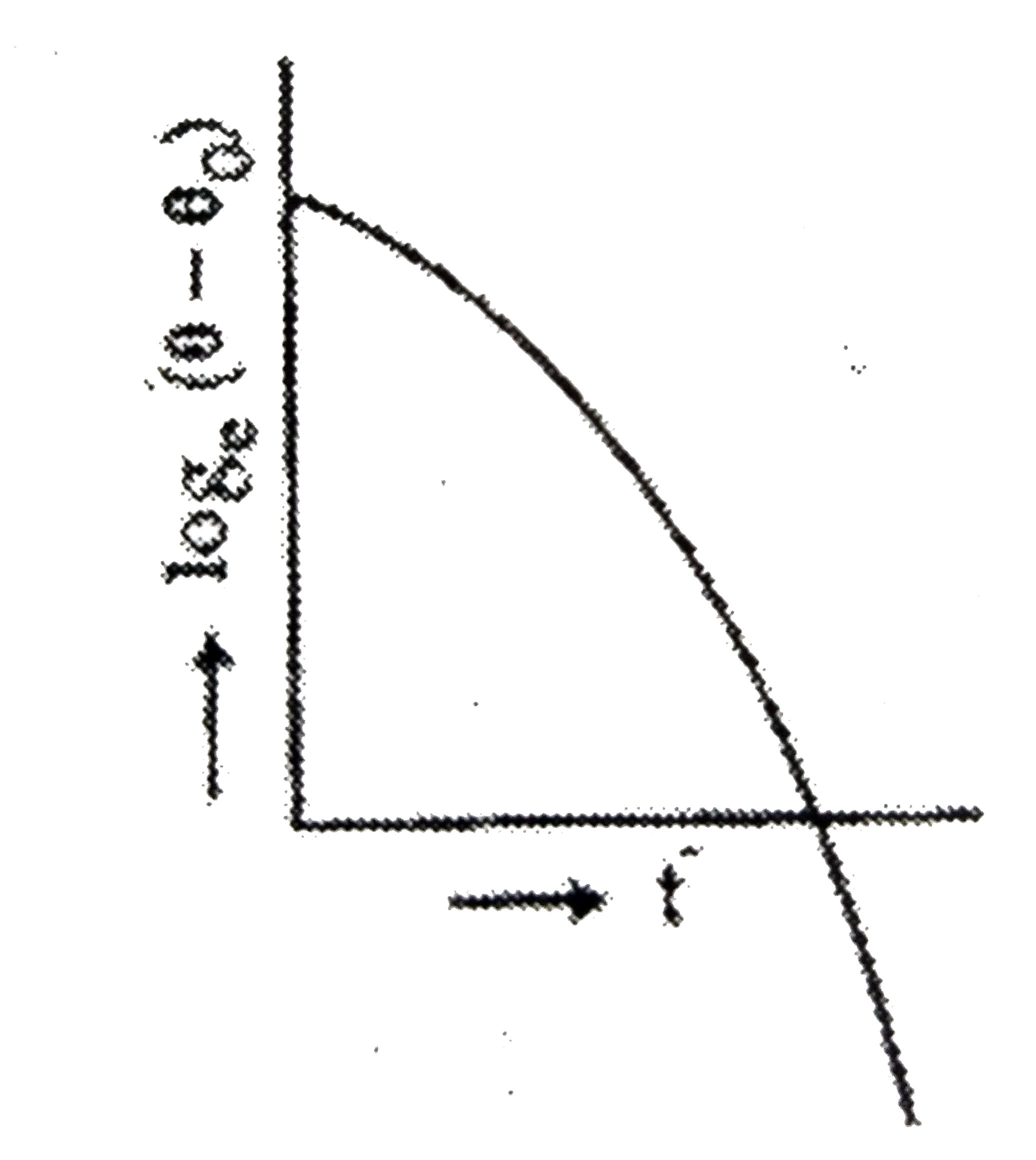

C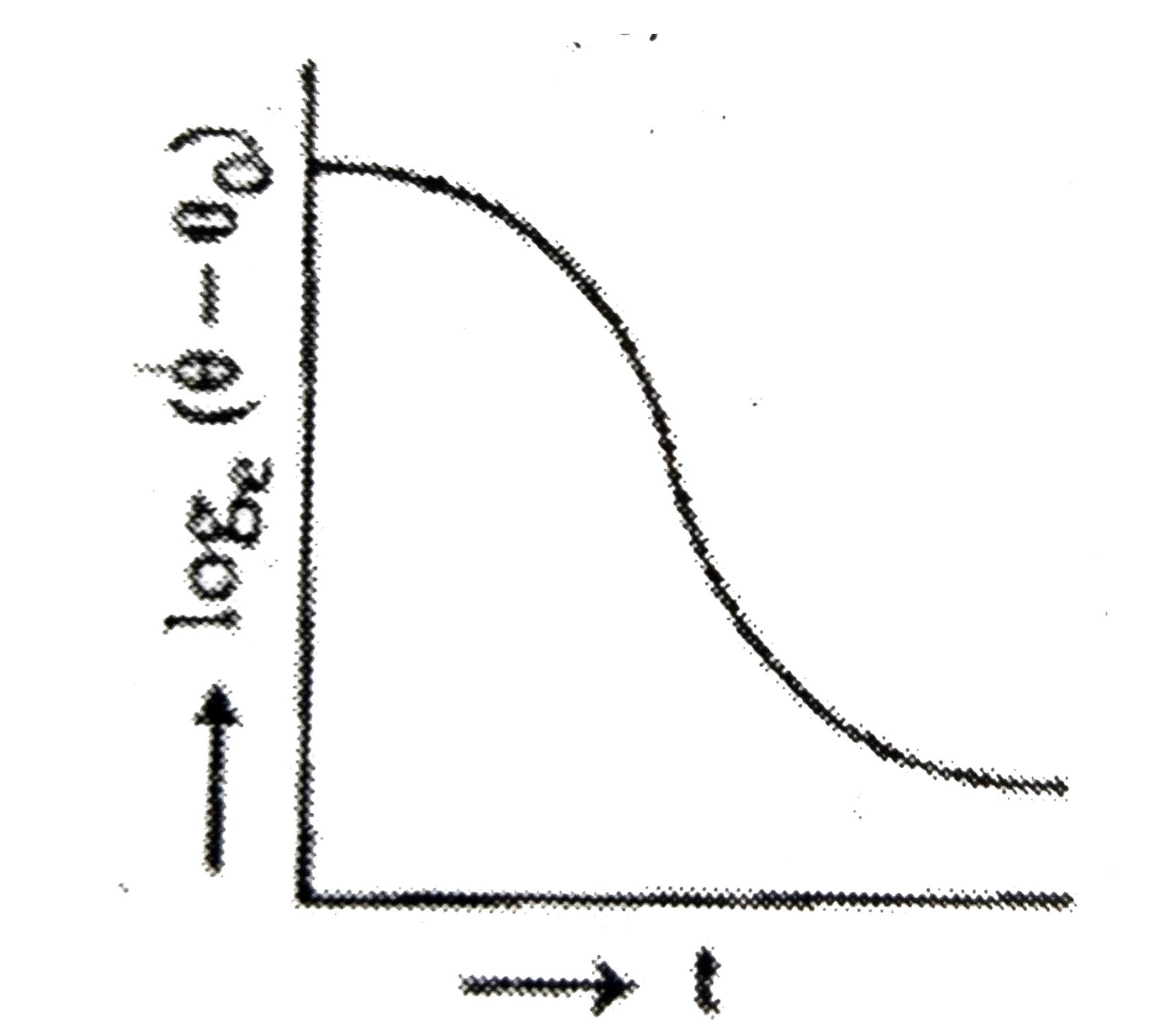

D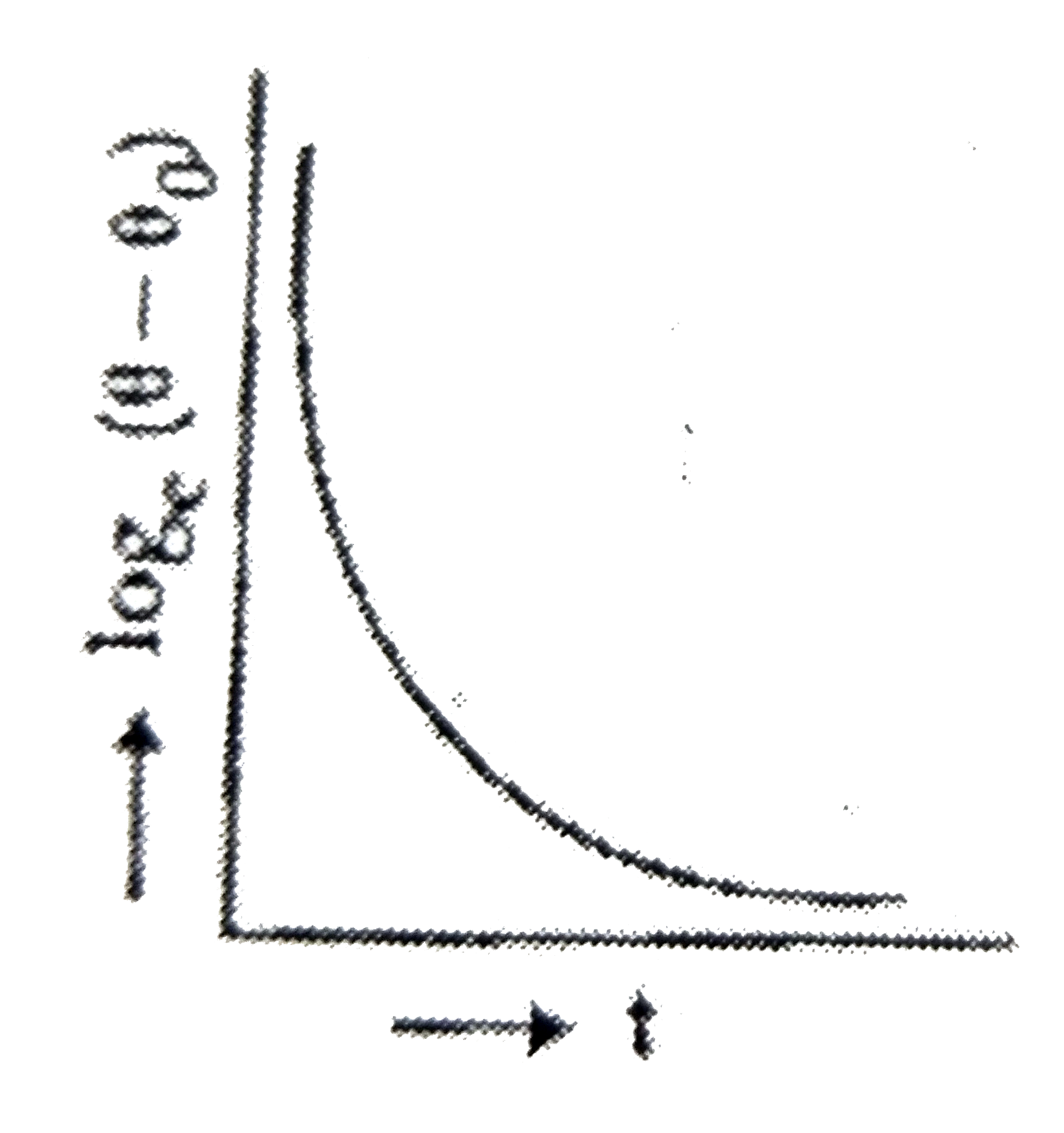

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem, we will use Newton's Law of Cooling, which states that the rate of heat loss of a body is directly proportional to the difference in temperature between the body and its surroundings. Let's go through the steps to derive the relationship and determine the correct graph.
### Step-by-Step Solution:
1. **Understanding Newton's Law of Cooling**:
According to Newton's Law of Cooling, the rate of change of temperature of the liquid is given by:
\[
\frac{d\theta}{dt} = -k(\theta - \theta_0)
\]
where \( \theta \) is the temperature of the liquid at time \( t \), \( \theta_0 \) is the temperature of the surroundings, and \( k \) is a positive constant.
2. **Rearranging the Equation**:
We can rearrange the equation to separate the variables:
\[
\frac{d\theta}{\theta - \theta_0} = -k \, dt
\]
3. **Integrating Both Sides**:
Now we will integrate both sides. The left side integrates with respect to \( \theta \) and the right side with respect to \( t \):
\[
\int \frac{d\theta}{\theta - \theta_0} = -k \int dt
\]
This gives us:
\[
\log(\theta - \theta_0) = -kt + C
\]
where \( C \) is the constant of integration.
4. **Exponentiating Both Sides**:
To eliminate the logarithm, we exponentiate both sides:
\[
\theta - \theta_0 = e^{-kt + C} = e^C e^{-kt}
\]
Let \( C' = e^C \), then:
\[
\theta - \theta_0 = C' e^{-kt}
\]
5. **Taking the Logarithm**:
We can express \( \log(\theta - \theta_0) \) in terms of \( t \):
\[
\log(\theta - \theta_0) = \log(C') - kt
\]
6. **Identifying the Form**:
This equation can be rearranged to:
\[
\log(\theta - \theta_0) = -kt + \log(C')
\]
This is in the form of a linear equation \( y = mx + b \) where:
- \( y = \log(\theta - \theta_0) \)
- \( x = t \)
- \( m = -k \) (the slope)
- \( b = \log(C') \) (the y-intercept)
7. **Graph Characteristics**:
The graph of \( \log(\theta - \theta_0) \) versus \( t \) will be a straight line with a negative slope (since \( k > 0 \)).
8. **Conclusion**:
Therefore, the correct graph will be a straight line that slopes downwards. Among the given options, the first graph represents this relationship correctly.
### Final Answer:
The correct graph between \( \log(\theta - \theta_0) \) and \( t \) is the first option.
|
Topper's Solved these Questions
JEE MAINS
JEE MAINS PREVIOUS YEAR ENGLISH|Exercise Chemistry|1 VideosView PlaylistJEE MAIN
JEE MAINS PREVIOUS YEAR ENGLISH|Exercise All Questions|452 VideosView PlaylistJEE MAINS 2020
JEE MAINS PREVIOUS YEAR ENGLISH|Exercise PHYSICS|250 VideosView Playlist
Similar Questions
Explore conceptually related problems
Two liquids of specific heat ratio 1:2 are at temperature 2theta and theta
Watch solution
In Newton's law of cooling (d theta)/(dt)=-k(theta-theta_(0)) the constant k is proportional to .
Watch solution
The correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
Watch solution
A solid body X of heat capacity C is kept in an atmosphere whose temperature is T_A=300K . At time t=0 the temperature of X is T_0=400K . It cools according to Newton's law of cooling. At time t_1 , its temperature is found to be 350K. At this time (t_1) , the body X is connected to a large box Y at atmospheric temperature is T_4 , through a conducting rod of length L, cross-sectional area A and thermal conductivity K. The heat capacity Y is so large that any variation in its temperature may be neglected. The cross-sectional area A of hte connecting rod is small compared to the surface area of X. Find the temperature of X at time t=3t_1.
Watch solution
The temperature of water in calorimeter is theta and the temperature of surrounding is theta_(0 ) ( lt theta) . Observation are recorded for temperature difference (theta- theta_0) and time t. The cooling curve is best represented in graph.
Watch solution
Themperature of a body theta is slightly more than the temperature of the surrounding theta_(0) its rate of cooling (R ) versus temperature of body (theta) is plotted its shape would be .
Watch solution
Evaluate: intsqrt(t a ntheta)\ d theta
Watch solution
Instantaneous temperature difference between cooling body and the surroundings obeying Newton's law of cooling is theta . Which of the following represents the variation of In theta with time t?
Watch solution
Two bodies A and B of equal masses, area and emissivity cooling under Newton's law of cooling from same temperature are represented by the graph: If theta is the instantaneous temperature of the body and theta_(0) , is the temperature of surroundings, then relationship between their specific heats is
Watch solution
If the system were lossing heat according to Newton's cooling law the temperature of the mixture would change with time according to (while heater was on) .
Watch solution