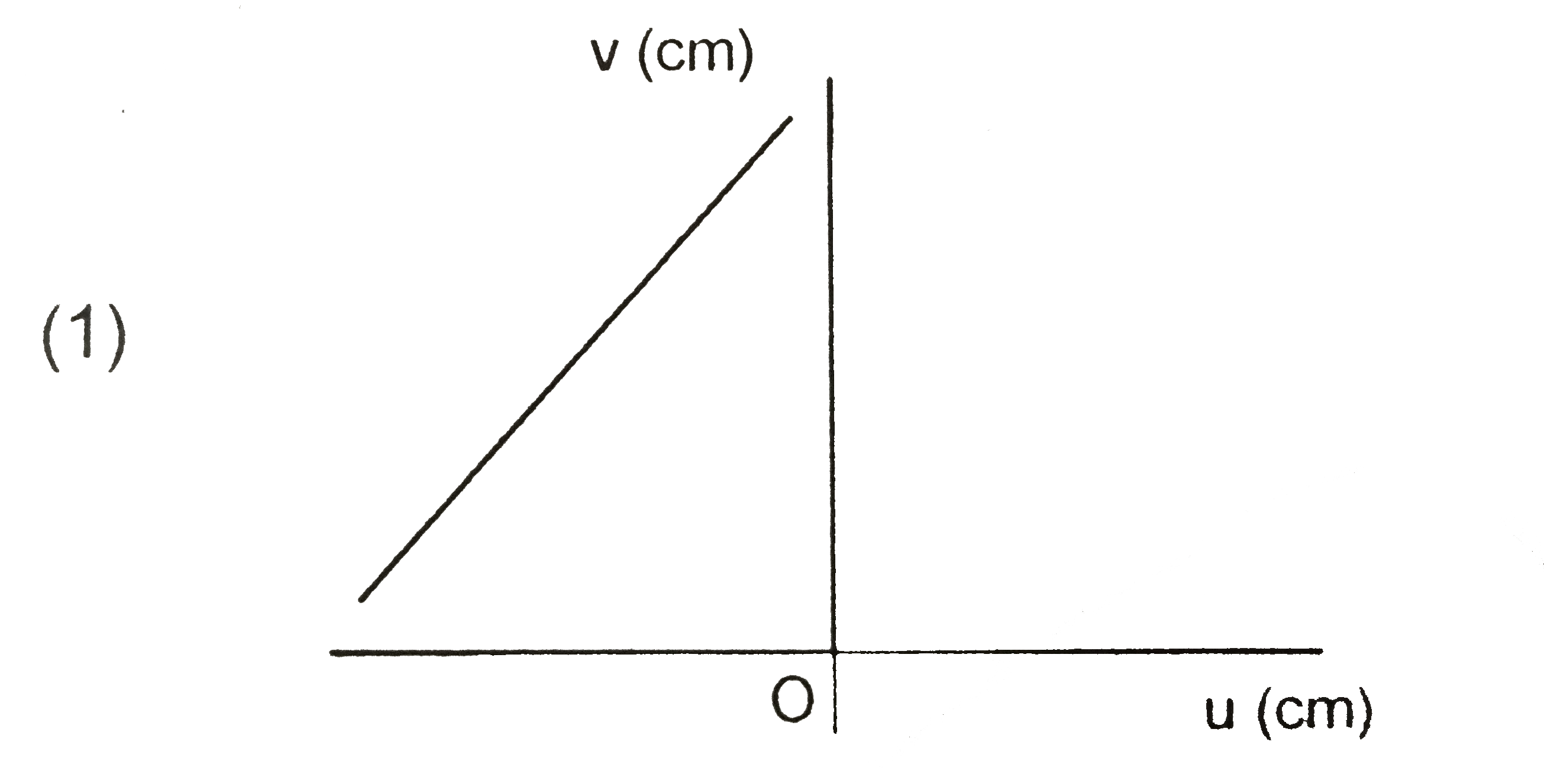
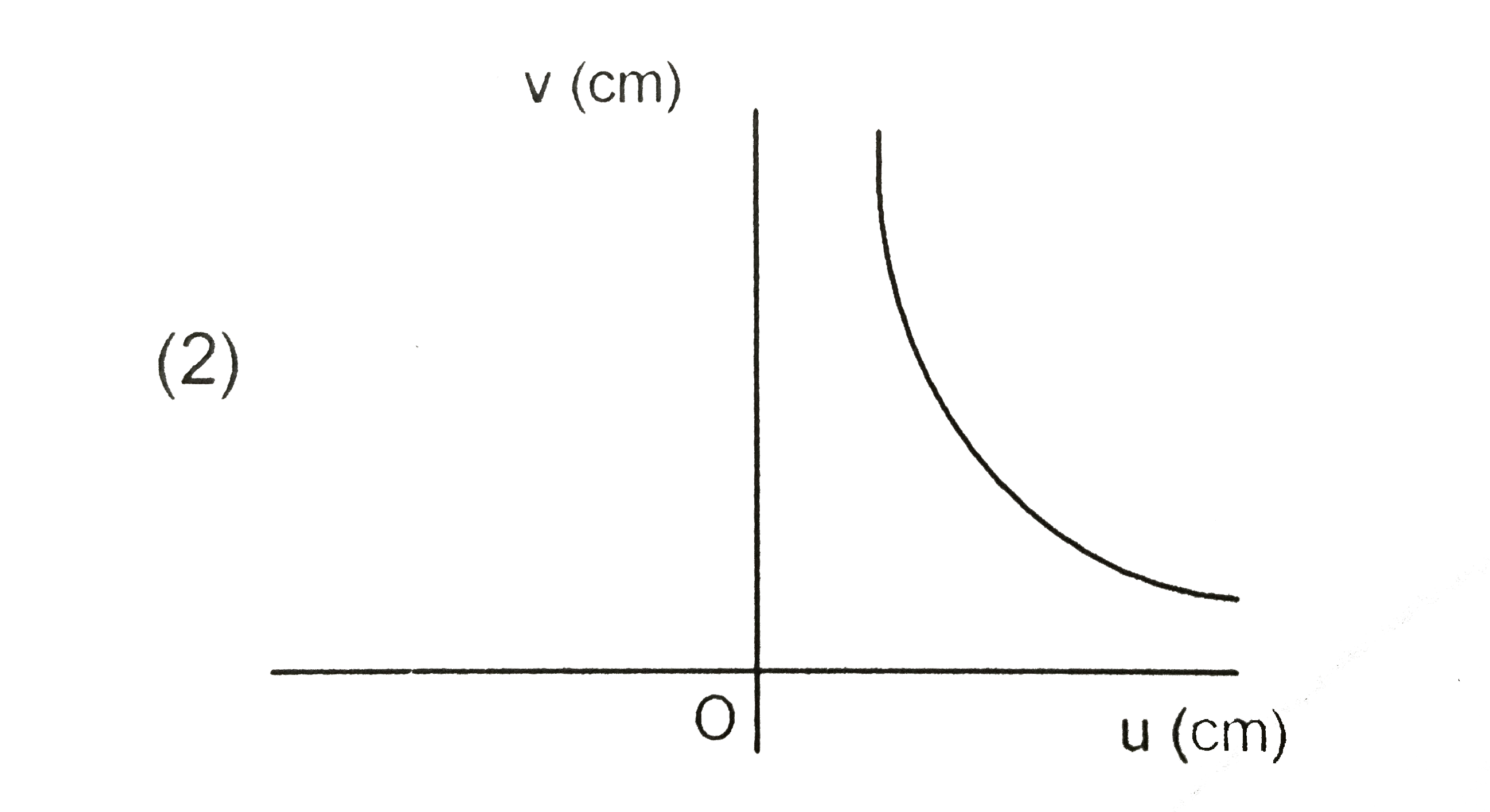
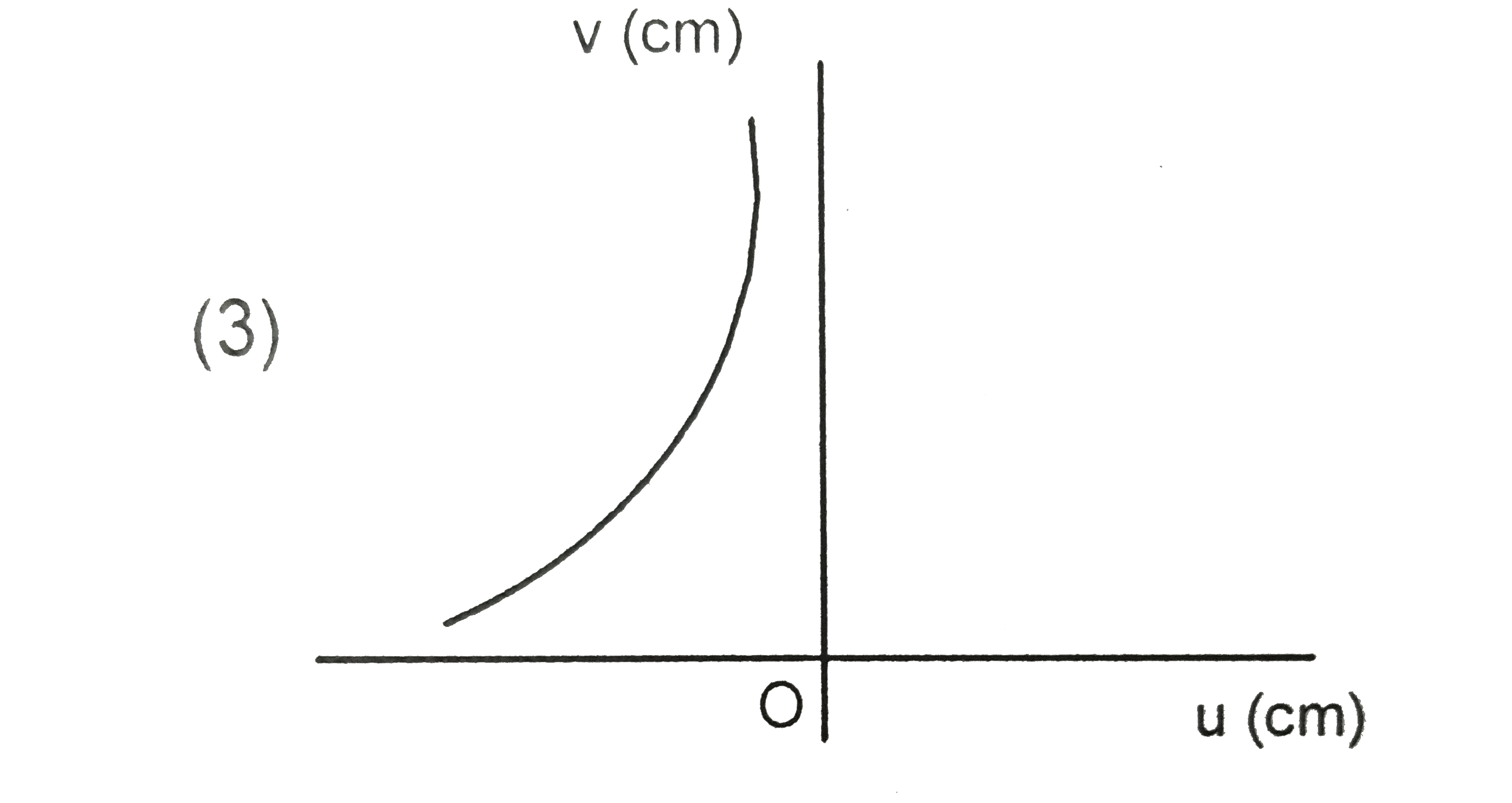
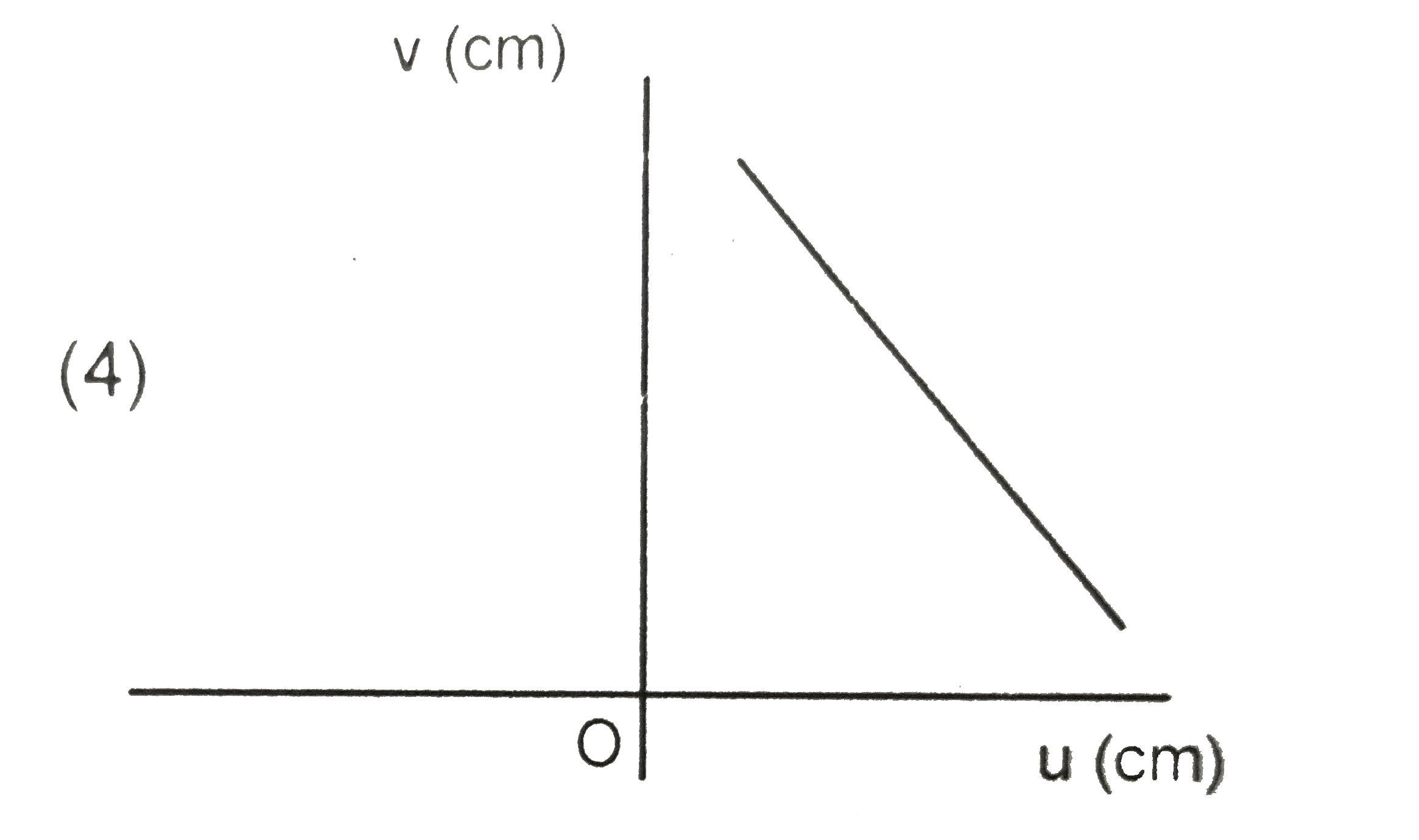
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
JEE MAINS
JEE MAINS PREVIOUS YEAR ENGLISH|Exercise Chemistry|1 VideosView PlaylistJEE MAIN
JEE MAINS PREVIOUS YEAR ENGLISH|Exercise All Questions|452 VideosView PlaylistJEE MAINS 2020
JEE MAINS PREVIOUS YEAR ENGLISH|Exercise PHYSICS|250 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems