Text Solution
Verified by Experts
|
Topper's Solved these Questions
LAWS OF MOTION
AAKASH SERIES|Exercise LONG ANSWER TYPE QUESTIONS|2 VideosView PlaylistLAWS OF MOTION
AAKASH SERIES|Exercise SHORT ANSWER TYPE QUESTION|2 VideosView PlaylistKINETIC THEORY OF GASES
AAKASH SERIES|Exercise Practice Exercise|15 VideosView PlaylistMECHANICAL PROPERTIES OF FLUIDS
AAKASH SERIES|Exercise EXERCISE-3|43 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
A
B
C
D
Submit
Similar Questions
Explore conceptually related problems
AAKASH SERIES-LAWS OF MOTION-PRACTICE EXERCISE
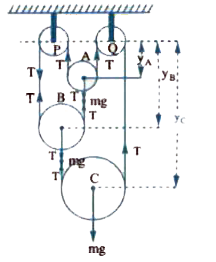
- In the pulley system shown in figure. P and Q are fixed pulleys while ...
Text Solution
|
Playing Now - A force of 50 N acts on a body of mass 10 kg at rest. Its velocity aft...
Text Solution
|
Play - A force of 10 N inclined to the horizontal at an angle of 60^(@) acts ...
Text Solution
|
Play - A constant retarding force of 20 N acts on a body of mass 5 kg moving ...
Text Solution
|
Play - A bullet of mass 0.005 kg moving with a speed of 200 ms^(-1) enters a ...
Text Solution
|
Play - A body of mass m falls from a height h(1) and rises to a height h(2). ...
Text Solution
|
Play - Two bodies of masses 4 kg and 16 kg at rest to acted upon by same forc...
Text Solution
|
Play - In a football match a ball is kicked by a player with a force of 25 N ...
Text Solution
|
Play - A ball of mass 10 gm dropped from a height of 5 m hits the floor and r...
Text Solution
|
Play - A body of mass 5 kg is at rest on a smooth horizontal surface. A horiz...
Text Solution
|
Play - A balloon of total mass 1000 Kg float motionless over the earth's surf...
Text Solution
|
Play - The horizontal speed of a jet of water is 100 cm/sec and 50 cm^(3) of ...
Text Solution
|
Play - A body of mass 2 kg has an initial velocity of 3 ms^(-1) along OE and ...
Text Solution
|
Play - A disc of mass 0.5 kg is kept floating horizontally in mid air by firi...
Text Solution
|
Play - A constant horizontal force of 20 N acts on a body on a smooth horizon...
Text Solution
|
Play - A gun of mass 10 Kg fires four bullets per second. The mass of each bu...
Text Solution
|
Play - A balloon has 5 gm of air. A small hole is pierced into it. The air es...
Text Solution
|
Play - A 1.5 kg hammer moving with a velocity of 10 m/s strikes a nail for 0....
Text Solution
|
Play - Six forces lying in a plane and forming angles of 60^(@) relative to o...
Text Solution
|
Play - A body is acted on by a force given by F = (10 + 2t) N. The impulse re...
Text Solution
|
Play - The linear momentum of a particle varies with time as p=a(0)+at+bt^(2)...
Text Solution
|
Play