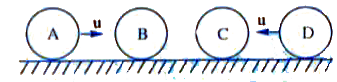Home
Class 11
PHYSICS
Four identical balls A,B,C and D are pla...

Four identical balls A,B,C and D are placed in a line on a frictionless horizontal surface. A and D are moved with same speed .u. towards the middle as shown. Assuming elastic collisions, find the final velocities.

Text Solution

Verified by Experts

The correct Answer is:
`V _(A) = u (to) ,V _(B) = 0, V _(C ) = 0 and V _(D) = u (to)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • COLLISIONS

    AAKASH SERIES|Exercise NUMERICAL EXERCISE ( LEVEL 2)|23 Videos

  • CENTRE OF MASS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))|3 Videos

  • ELASTICITY

    AAKASH SERIES|Exercise Questions for Descriptive Answers|10 Videos

Similar Questions

Explore conceptually related problems

A bullet of mass m moving with velocity u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown in the figure. Assume that the cylinder rolls without slipping. The angular velocity of the cylinder is omega and the final velocity of the bullet is V, then omega=(4"mu")/((8m+aM)R),V=("8mu")/((8m+bM)) then ab is

Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig. 6. 14) is a possible result after collision?

Knowledge Check

  • Two identical balls of mass M and mradius R each are placed on a frictionless plane. One of the balls is at rest while the second moves at a velocity v towards the first ball tangentially. The two balls stick together on collision. Then

    A
    the speed of the centre of mass does not change because of the collision
    B
    the angular velocity of the system after the collision is `(5v)/(14R)`
    C
    the kinetic energy of the system after the collision is `3/7"Mv"^(2)`
    D
    some energy is lost during the collision.

  • Four persons A,B,C and D intially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always , the person will meet after time

    A
    `d/v `
    B
    `(sqrt2d)/(v) `
    C
    `(d)/(2v)`
    D
    `(d)/(sqrt2v)`

  • Four persons A,B,C and D intially at the corners of a square of side of length d. If every person starts moving with same speed v such that each one faces the other always , the person will meet after time

    A
    `d/v `
    B
    `(sqrt2d)/(v) `
    C
    `(d)/(2v)`
    D
    `(d)/(sqrt2v)`

    • Similar Questions

    Explore conceptually related problems

    Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V . If the collision is elastic, which of the following (fig.) is a possible result after collision ?

    Two smooth spheres A and B, of equal radius but masses m and M, are free to move on a horizontal table. A is projected with speed u towards B which is at rest. On impact, the line joining their centres is inclined at an angle theta to the velocity of A before impact. If e is the coefficient of restitution between the spheres, find the speed with which B begins to move. If A.s path after impact is perpendicular to its path before impact, show that tan ^(2) theta = (eM-m)/(M +m).

    Four particles of masses m, 2m, 3m and 4m are placed at the vertices of a rectangle ABCD as shown in the figure. The particles move from A to B, B to C. C to D and D to A respectively. In this process find the displacement of centre of mass of the system.

    Four charges of +q, +q, +q and +q are placed at the corners A, B, C and D of a square. Find the resultant force on the charge at D.

    A uniform rod of length L rests on a frictionless horizontal surface. The rod is pivoted about a fixed frictionless axis at one rod. The rod is initially at rest. A bullet travelling parallel to the horizontal surface and perpendicular to the rod with speed V_(0) strikes the rod at its centre and becomes embedded in it. The mass of the bullet is one-sixth of the mass of the rod. The final angular velocity of the rod is omega and the ratio of the kinetic energy of the system after collicion to the kinetic energy of the bullet before collision is 1/x where x is

    Home
    Profile