Home
Class 9
MATHS
Prove that the line segment joining the ...

Prove that the line segment joining the centres of two intersecting circles subtends equal angles at the two points of intersection.

Answer

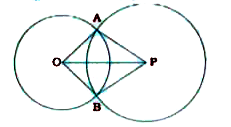
Step by step text solution for Prove that the line segment joining the centres of two intersecting circles subtends equal angles at the two points of intersection. by MATHS experts to help you in doubts & scoring excellent marks in Class 9 exams.

Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CIRCLES

    KUMAR PRAKASHAN|Exercise SKILL TESTING EXERCISE|7 Videos

  • CIRCLES

    KUMAR PRAKASHAN|Exercise MULTIPLE CHOICE QUESTIONS (MCQ.s)|14 Videos

  • CIRCLES

    KUMAR PRAKASHAN|Exercise EXERCISE 10.5|12 Videos

  • BOARD'S SAMPLE QUESTION PAPERS (QUESTION PAPER 1 : FOR THE FIRST TEST)

    KUMAR PRAKASHAN|Exercise Section D (Solve the following) |4 Videos

  • CONSTRUCTIONS

    KUMAR PRAKASHAN|Exercise Skill Testing Exercise|2 Videos

Similar Questions

Explore conceptually related problems

If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.

Line segment joining the centre to any point on the circle is a radius of the circle

Prove that line segment joining mid points of the two sides of the triangle is parallel to third side.

Recall that two circles are congruent if they have the same radii. Proe that equal chords of congruent circles subtend equal angles at their centres.

Prove that if chords f congruent circles subtend equal angles at their centres, then the chords are equal.

prove that the line segment joining the midpoints of two opposite sides of a parallelogram divides the parallelogram into two parallelograms with equal area.

The line segment joining the mid-points of any two sides of a triangle in parallel to the third side and equal to half of it.

Find the ratio in which the y-axis divides the line segment joining the points (5,-6) and (-1, -4) . Also find the point of intersection.

Prove that opposite side of a quadrilateral circumscribing a circle subtend supple. Mentary angle at the center of the circle.

If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.

Home
Profile