Magnetic flux `phi_(B)` through a plane of area 'A' placed in a uniform magnetic field `vceB` is given as:
`phi_(B)= vceB.vceA = BA cos theta`
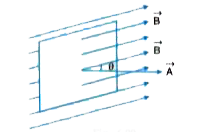
where `theta` is the angle between `vceB` and `vceA`. The above relatio can be extended to curved surfaces and non-uniform fields. In general, if the magnetic field has different magnitudes an directions at various parts of a surface, then the magnetic flux through the surface is given by
`phi_(B)=int vec B.dvecA`
On the basis of the experimental observations, Faraday concluded that an emf is induced in a coil when magnetic flux through the coil changes with time. Faraday stated his conclusions in the form of a law called Faraday's law of electromagnetic induction. As per this law, the induced emf is given by
`varepsilon = -(dphi_(B))/dt`
The negative sign in the expression indicates the direction of induced emfe and hence the direction of current in a closed loop.
In the case of a closely would coil of N turns, change of flux associated with each turns is the same and so that total induced emf is given by `varepsilon=-N(dphi_(B))/dt`
From above relations it is clear that the magnetic flux can be changed by changing any one or more of the terms `vceB, vceA and theta`.
(a) Give SI unit of magnetic flux.
(b) How is it related to tesla ?
(c) Obtain dimensional formula of magnetic flux.
(d) A loop of area `4 xx 10^(-3)m^(2)` is placed with its plane perpendicular to a uniform magnetic field of 0.02 T. If the loop is quickly removed from the magnetic field within a time of 2 ms, what is the magnitude of induced emf across the two ends of the loop ?
(e) If the resistance of the loop be `0.2Omega` and a sensitive milliammeter be connected between the two ends of loop, what will be the reading of milliammeter?
