Home
Class 10
MATHS
In DeltaABC, seg AD bot seg BC, DB=3...

In `DeltaABC`,
seg `AD bot` seg `BC`,
`DB=3CD`.
Prove that `2AB^(2)=2AC^(2)+BC^(2)`.

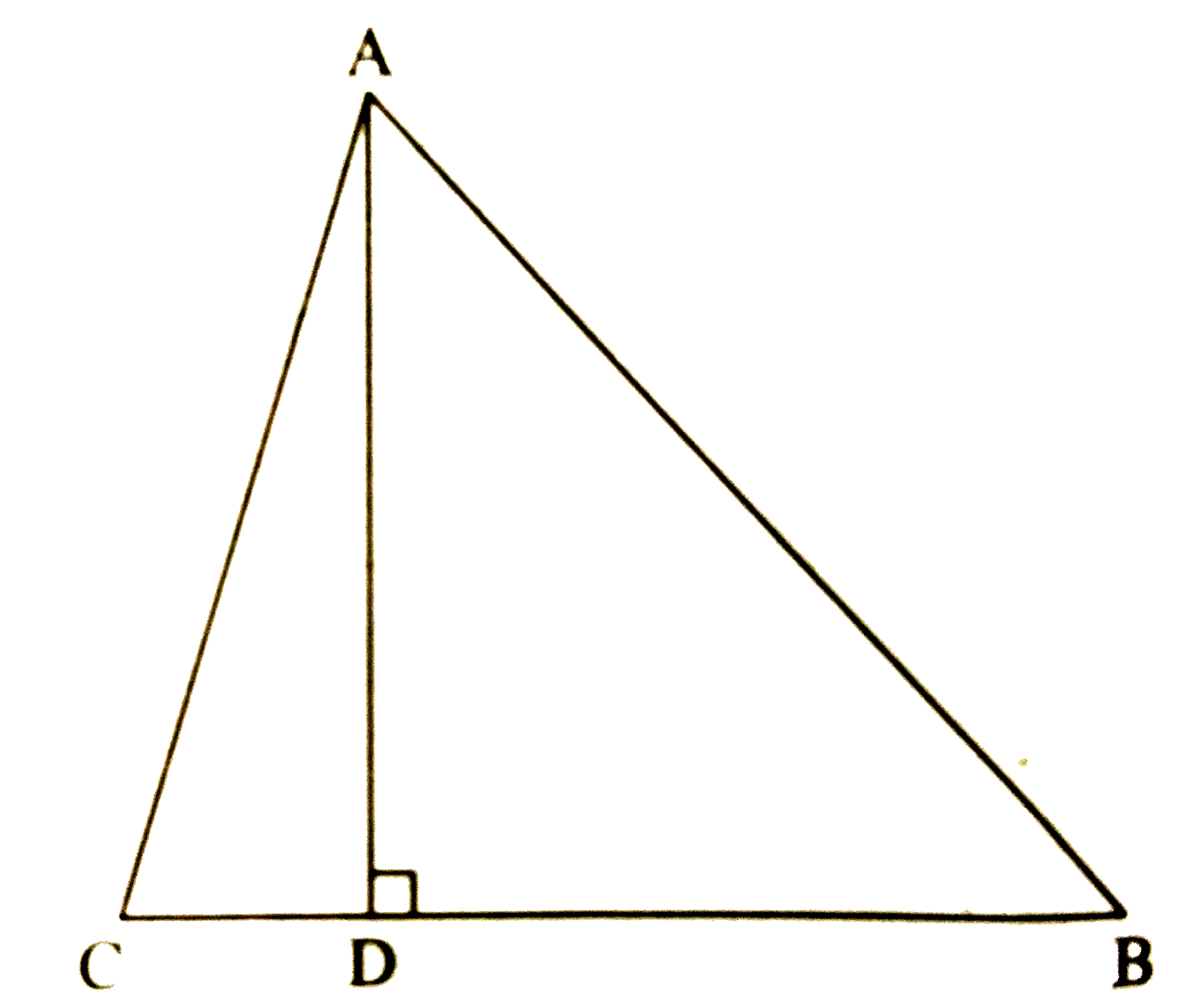
Text Solution

Verified by Experts

The correct Answer is:
`therefore2AB^(2)=2AC^(2)+BC^(2)`
Promotional Banner

Topper's Solved these Questions

  • PYTHAGORAS THEOREM

    TARGET PUBLICATION|Exercise Problem set-27|1 Videos

  • PYTHAGORAS THEOREM

    TARGET PUBLICATION|Exercise Problem set-30|1 Videos

  • PYTHAGORAS THEOREM

    TARGET PUBLICATION|Exercise Problem set-10|16 Videos

  • PROBABILITY

    TARGET PUBLICATION|Exercise Try This|1 Videos

  • QUADRATIC EQUATIONS

    TARGET PUBLICATION|Exercise Chapter Assessment|39 Videos

Similar Questions

Explore conceptually related problems

In DeltaABC, if M is the midpiont of BC and seg AM bot seg BC, then prove that prove that AB^(2)+AC^(2)=2AM^(2)+2BM^(2).

In triangle ABC , seg AD_|_side BC , B-D-C. Prove that AB^2+CD^2=BD^2+AC^2

In DeltaABC,angleABC=135^(@) . Prove that : AC^(2)=AB^(2)+BC^(2)+4A(DeltaABC) .

In adjoining figure, in DeltaABC , seg AD and seg BE are altitudes and AE = BD. Prove that seg AD = seg BE.

In DeltaABC , ray BD bisects /_ABC . A-D-C , side DE|| side BC , A-E-B . Prove that, (AB)/(BC)=(AE)/(EB) . Complete the activity by filling the boxes. In DeltaABC , ray BD is the bisector of /_ABC :.(AB)/(BC)=square ....... (I) (By angle bisector theorem) In DeltaABC , seg DE|| side BC :.(AE)/(EB)=(AD)/(DC) ........ (II) square :.(AB)/(square)=(square)/(EB) .......[From (I) and (II) ]

In the adjoining figure, in DeltaABC , point D is on side BC such that, angleBAC = angleADC . Prove that, CA^2 = CB xx CD .

In triangle ABC , angle BAC = 90^(@) , seg BL and seg CM are medians of triangle ABC . Then prove that 4 (BL^(2) + CM^(2)) = 5 BC^(2)

In an equilateral triangle ABC,the side BC is trisected at D.Prove that: 9AD^2=7AB^2 .

In the figure , point T is in the interior of rectangle PQRS . Prove that, TS^(2)+TQ^(2)=TP^(2)+TR^(2) (As shown in the figure, draw seg AB|| side SR and A-T-B .)

In the adjoining figure,seg DE abs() side AC and seg DC abs() side AP. Prove that (BE)/(EC) = (BC)/(CP) .