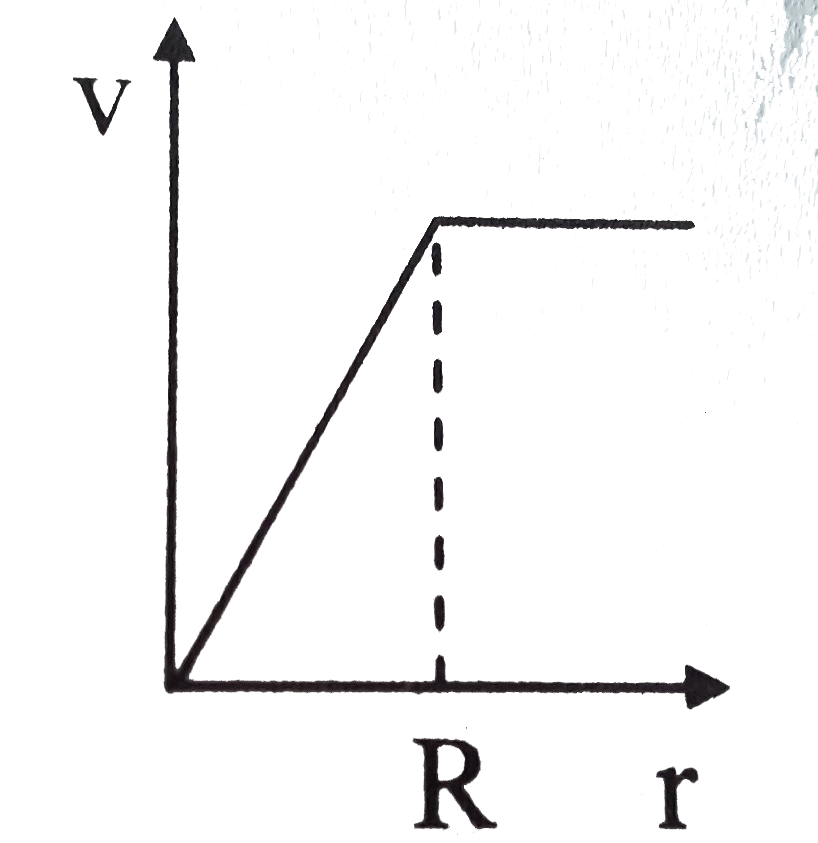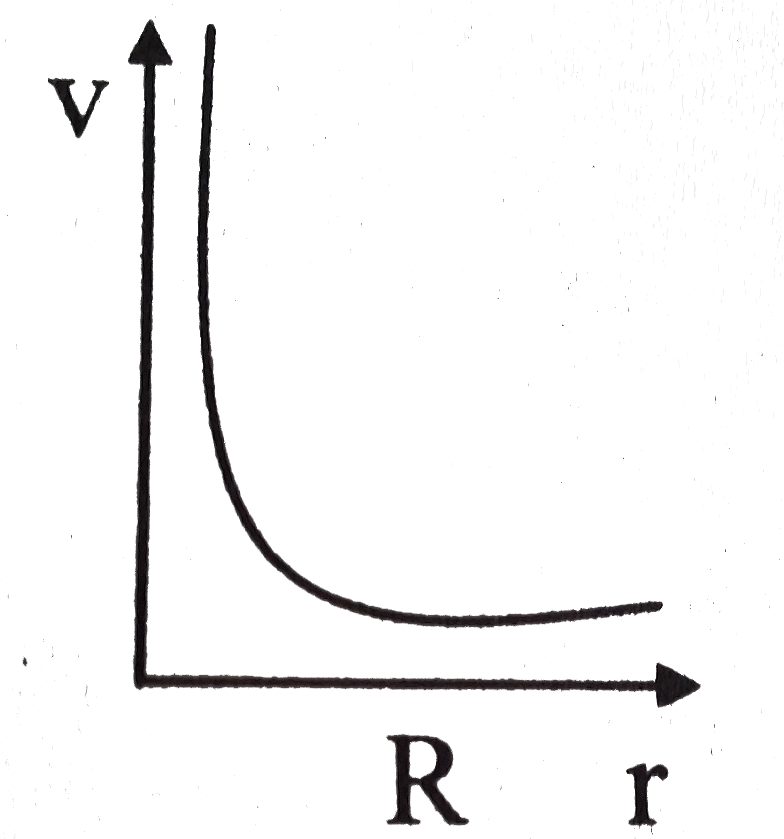Recommended Questions
- A spherically symmetric gravitational system of particles has a mass d...
04:35
|
Playing Now - A spherically symmetric gravitational system of particles has a mass d...
03:38
|
Play - एक गोलाकार सममित (symmetrical) गुरुत्वीय के समूह का द्रव्यमान घनत...
03:25
|
Play - The volume charge density in a spherical ball of radius R varies with ...
Text Solution
|
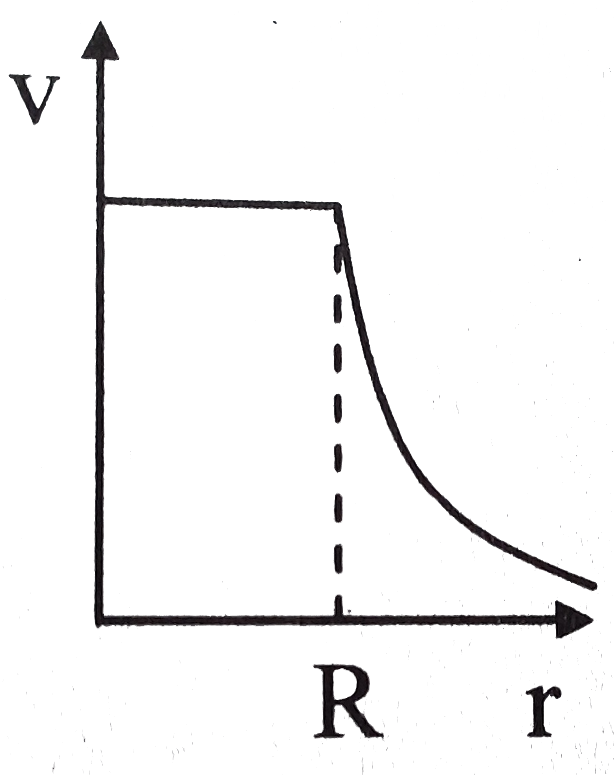
Play - Mass density of sphere having radius R varies as rho = rho0(1-r^2/R^2)...
08:26
|
Play - एक परीक्षण कण, द्रव्यमान घनत्व rho(r )=(K)/(r^(2)) से उत्पन्न गुरुत्वी...
05:38
|
Play - Charge density of a sphere of radius R is rho = rho0/r where r is dist...
04:25
|
Play - Mass density of sphere having radius R varies as rho = rho0(1-r^2/R^2)...
06:13
|
Play - Charge density of a sphere of radius R is rho = rho0/r where r is dist...
03:12
|
Play