Text Solution
Verified by Experts
|
Topper's Solved these Questions
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
MBD PUBLICATION|Exercise QUESTION BANK|76 VideosView PlaylistCONTINUITY AND DIFFERENTIABILITY
MBD PUBLICATION|Exercise QUESTION TYPE|4 VideosView Playlist
Similar Questions
Explore conceptually related problems
MBD PUBLICATION-CONIC SECTIONS-QUESTION BANK
- Find the equation of circles determined by the following conditions. T...
05:02
|
Play - Find the equation of circles determined by the following conditions. C...
08:37
|
Play - Find the equation of circles determined by the following conditions. C...
03:22
|
Playing Now - Find the equation of circles determined by the following conditions. C...
07:42
|
Play - Find the centre and radius of the following circles : x^2 + y^2 + 6x -...
03:21
|
Play - Find the centre and radius of the following circles : ax^2 + ay^2 + 2g...
06:06
|
Play - Find the centre and radius of the following circles : 4x^2 + 4y^2 - 4x...
05:50
|
Play - Find the centre and radius of the following circles : a(x^2 + y^2) - b...
05:25
|
Play - Obtain the equation of circles passing through the following points an...
06:22
|
Play - Obtain the equation of circles passing through the following points an...
12:19
|
Play - Obtain the equation of circles passing through the following points an...
09:46
|
Play - Obtain the equation of circles passing through the following points an...
11:46
|
Play - Find the equation of the circles circumscribing the triangles formed b...
10:56
|
Play - Find the equation of the circles circumscribing the triangles formed b...
09:17
|
Play - Find the equation of the circles circumscribing the triangles formed b...
12:03
|
Play - Find the equation of the circles circumscribing the triangles formed b...
10:16
|
Play - Find the coordinates of the points where the circle x^2 + y^2 -7x - 8y...
06:09
|
Play - Find the equation of the circle passing through the point (1, -2) and ...
05:48
|
Play - Find the equation of the circle whose ends of a diameter are the point...
07:23
|
Play - Find the equation of the circle inscribed inside the triangle formed b...
05:41
|
Play
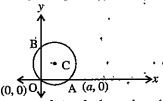 As it passes through the points (a, 0) and (0, 0).
As it passes through the points (a, 0) and (0, 0).