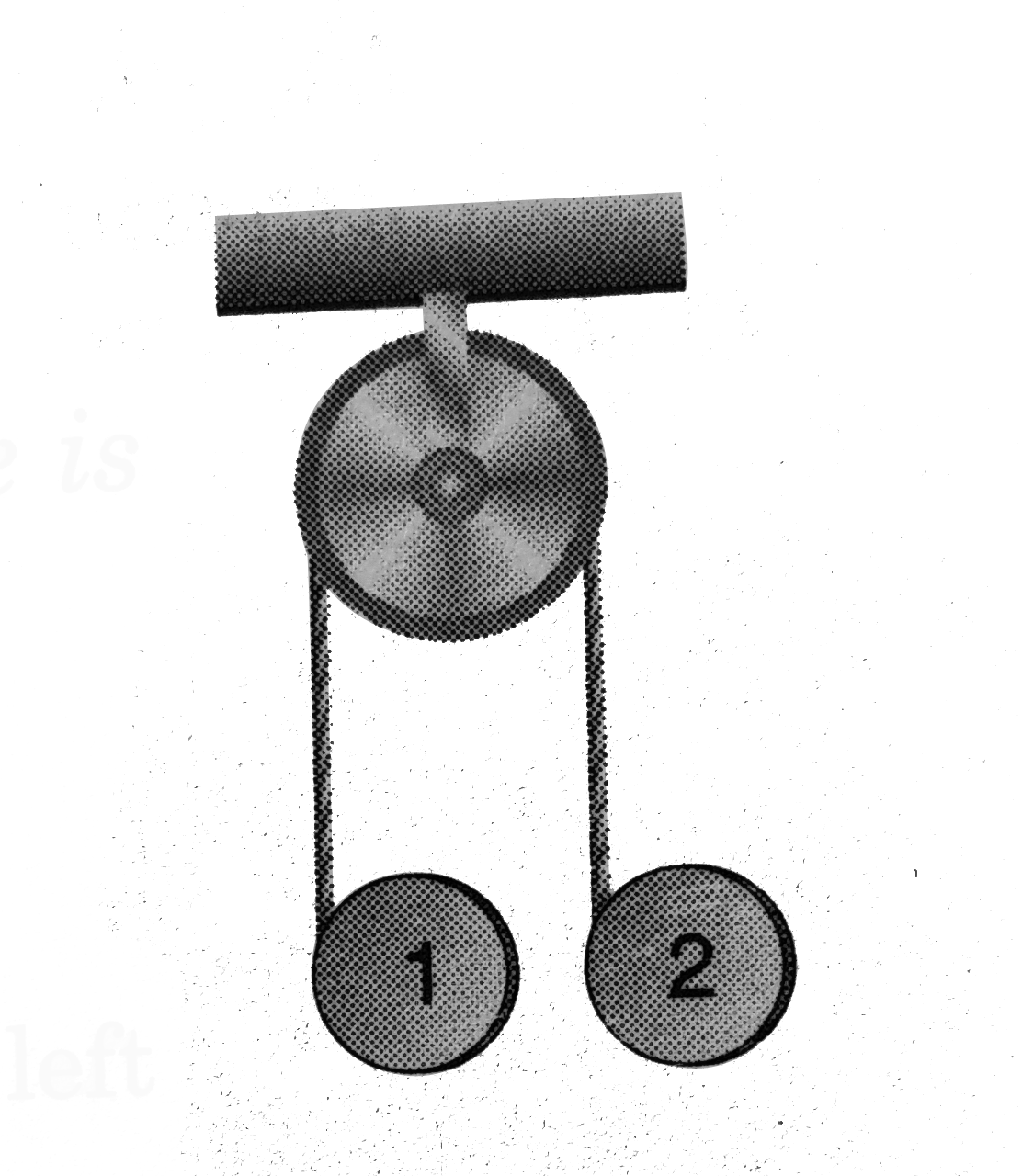A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.

Explanation

Let R be the radius of the disc and `T_(1)` and `T_(2)` be the tensions in the left and right segments of the rope
Acceleration of disc 1,
`a_(1)=(mg-T_(1))/(m)` ..(i)
Acceleration of disc 2, `a_(2)=(mg-T_(2))/(m)` ..(ii)
Angular acceleration of disc 1, `alpha_(1)=(tau)/(I)=(T_(1)R)/((1)/(2)mR^(2))=(2T_(1))/(mR)` ..(iii)
Similarly, angular acceleration of disc 2, `alpha_(2)=(2T_(2))/(mR)` ..(iv)
Both `alpha_(1)` and `alpha_(2)` are clockwise.
Angular acceleration of pulley
`alpha=((T_(2)-T_(1))R)/((1)/(2)mR^(2))=(2(T_(2)-T_(1)))/(mR)` ..(v)
For no slipping `Ra_(1)=a_(2)-Ralpha_(2)=Ralpha` ..(vi)
Solving these equation we get
`a=0` and `a_(1)=a_(2)=(2g)/(3)`
Alternate solution
As both the discs are in identical situation `T_(1)=T_(2)` and `alpha=0` i.e, each of the discs falls independently and identically. therefore this is exactly similar to the problem shown in figure.