A source of sound of frequency `f` is approaching towards a wall with speed `upsilon_(s)` . Speed of sound is `upsilon` . Three observers `O_(1)` , `O_(2)` and `O_(3)` are at different locations as shown . Find the beat frequency as observed by three different observers.

Answer

B

Explanation

For reflected sound we can take wall as a plane mirror.



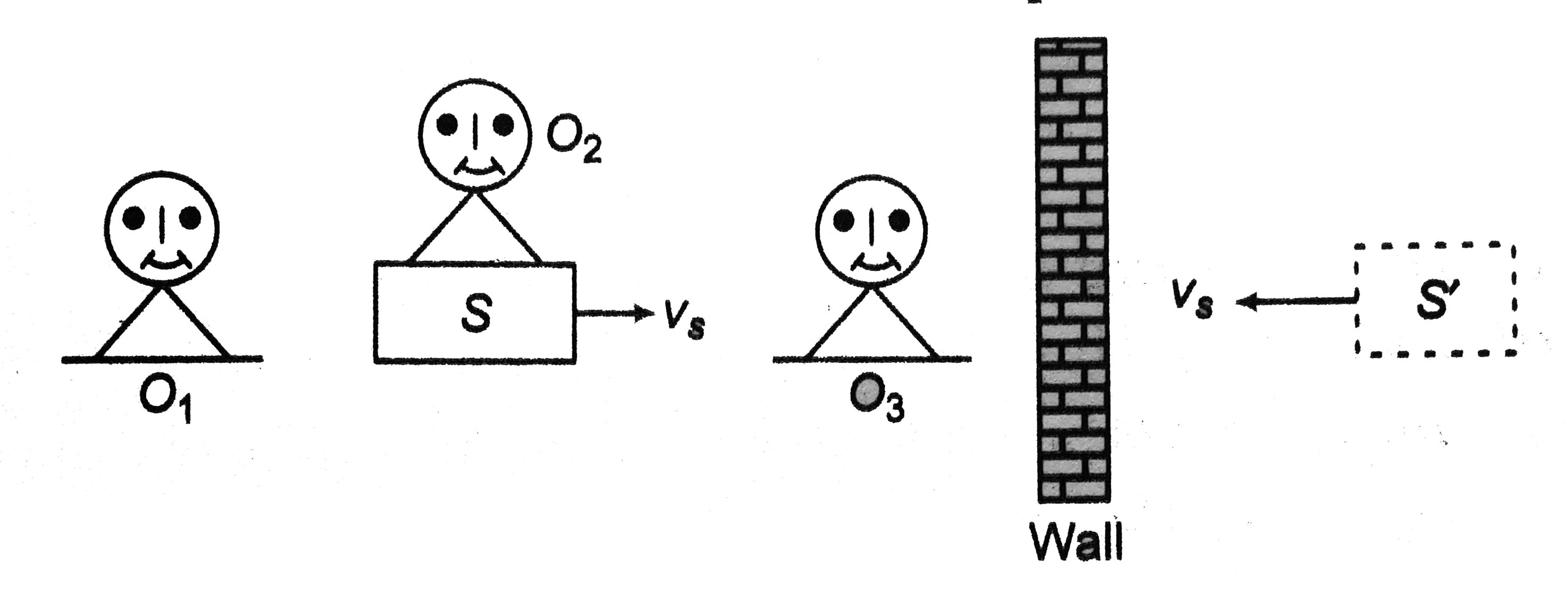
Observer `O_(1)S` is receding from `O_(1)` and `S` ' i`((2upsilon_(s))/(upsilon- upsilon_(s))) f` approaching towards him. So,
`f_(s')gtf_(s)`
`f_(b) = f_(s') - f_(s)`
= `f (upsilon/(upsilon - upsilon_(s)))- f(upsilon/(upsilon + upsilon_(s)))`
= `((2 upsilon upsilon_(s))/(upsilon^(2) - upsilon_(s)^(2))) f`
Observer `O_(2)` `O_(2)` has no relative motion with `S` . Therefore, there will be no change in the frequency of direct sound from `S` . Further, `O_(2)` and `S` ' are approaching towards each other. Therefore, the frequency of reflected sound will increase.
`f_(b) = f_(s') -f_(s)`
= `f ((upsilon + upsilon_(02))/(upsilon - upsilon_(s))) - f`
But `upsilon_(02) = upsilon_(s)`
`:. f_(b) = f ((upsilon + upsilon_(s))/(upsilon - upsilon_(s))) - f`
= `((2upsilon_(s))/(upsilon- upsilon_(s))) f`
Observer `O_(3)S` and `s'` both approaching towards `O_(3)` . SO, both frequenceies will increase. But after the increease they are equal . So, beat frequency will be zero.
`f_(s) = f_(s')= f ((upsilon)/(upsilon - upsilon_(s)))`
`:. f_(b) = f_(s) - f_(s') = 0`