Find equivalent capacitance between poin...

Find equivalent capacitance between points `A` and `B`. [Assume each conducting plate is having same dimensions and neglect the thickness of the plate `(epsilon_0A)/d=7muF` where A is area of plate]` `

`7muF`

`11muF`

`12muF`

`15muF`

Text Solution

Verified by Experts

The correct Answer is:

`C=(epsilon_0A)/d=7muF`
The equivalent circuit is as shown in figure.

`C_(AB)=11/7 C=11/7(7muF)`
`=11muF`

Topper's Solved these Questions

CAPACITORS
DC PANDEY ENGLISH|Exercise OBJECTIVE_TYPE|1 Videos
CAPACITORS
DC PANDEY ENGLISH|Exercise OBJECTIVE_TYPE|1 Videos
ATOMS
DC PANDEY ENGLISH|Exercise MEDICAL ENTRANCES GALLERY|42 Videos
COMMUNICATION SYSTEM
DC PANDEY ENGLISH|Exercise Subjective|11 Videos

Similar Questions

Explore conceptually related problems

Find out equivalent capacitance between A and B. (take each plate Area = A)

Find the equivalent capacitance between point a and b in the following arrangement of the plates .

Find the equivalent capacitance between A and B . A : area of each plate, d : separation between the plates.

Find out equivalent capacitance between A and B. (take each plate Area = A and distance between two conjugative plates is d)

The equivalent capacitance between P and Q in the figure is (area of each plate is A and separation between two consecutive plates is d)

The equivalent capacitance of the arrangement shown in figure, if A is the area of each plate is

Derive an expression for the capacitance of a parallel plate capacitor in terms of the areas of the plates and the distance between them. Assume there is a vacuum in between the plates with the electric field between the plates E=(sigma)/(epsilon_(0)) (where the symbols have their usual meaning).

Find the capacitance between A and B if three dielectric slabs of dielectric constants K_(1) area A _(2) and thickness d_(2) ) are inserted between the plates of a parallel late capacitor of plate area A. (Given that the distance between the two plates is d_(1)=d_(2)+d_(2) .) .

Find out the capacitance of parallel plate capacitor of plate area A and plate separation d.

Force between two conducting large plates , with charges Q and Q/2 as shown in the figure, is (Area of each face of plate =A)

DC PANDEY ENGLISH-CAPACITORS-Exercise

Four ways of making a network of five capacitor of the same value are ...
Text Solution
|
The equivalent capacitance of the arrangement shown in figure, if A is...
Text Solution
|
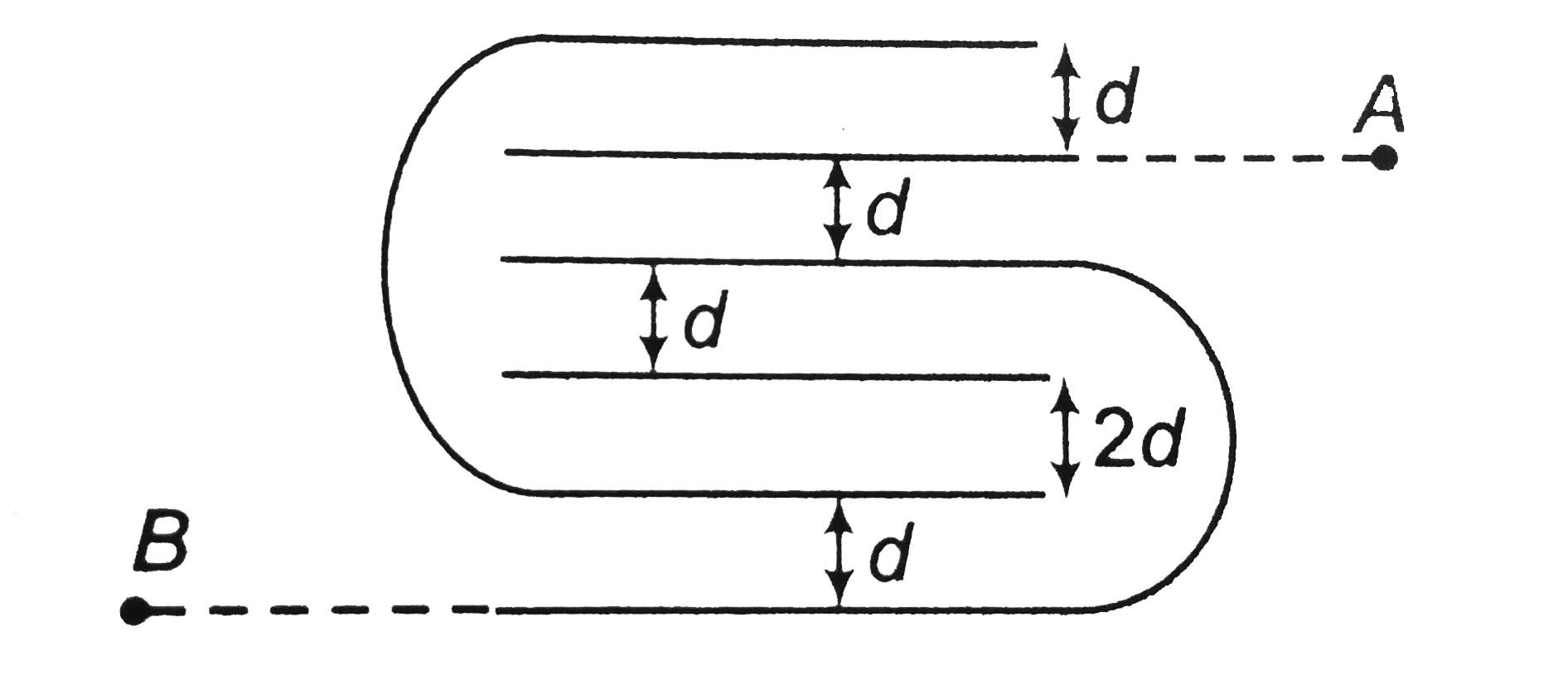
Find equivalent capacitance between points A and B. [Assume each condu...
Text Solution
|
Two metallic plates are kept parallel to one another and charges are g...
Text Solution
|
Charges 2q and -3q are given to two identical metal plates of area of ...
Text Solution
|
Find the charged stored in all the capacitors
Text Solution
|
Find the charge stored in the capacitor.
Text Solution
|
Find the charge stored in the capacitor.
Text Solution
|
A 1muF capacitor and a 2µF capacitor are connected in series across a ...
Text Solution
|
A 100muF capacitor is charged to 100 V. After the charging, battery is...
Text Solution
|
An Uncharged capacitor C is connected to a battery through a resistanc...
Text Solution
|
How many time constants will elapse before the current in a charging R...
Text Solution
|
A capacitor of capacitance C is given a charge q0. At time t = 0 it is...
Text Solution
|
A capacitor of capacitance as C is given a charge Q. At t=0,it is conn...
Text Solution
|
Determine the current through the battery in the circuit shown in figu...
Text Solution
|
For the circuit shown in figure, find (a) the initial current throug...
Text Solution
|
Find equivalent capacitance between points A and B,
Text Solution
|
A 4.00 muF capacitor and a 6.00muF capacitor are connected in parallel...
Text Solution
|
The plates of a parallel plate capacitor have an area of 90 cm^(2) eac...
Text Solution
|
The dielectric to be used in a parallel-plate capacitor has a dielectr...
Text Solution
|