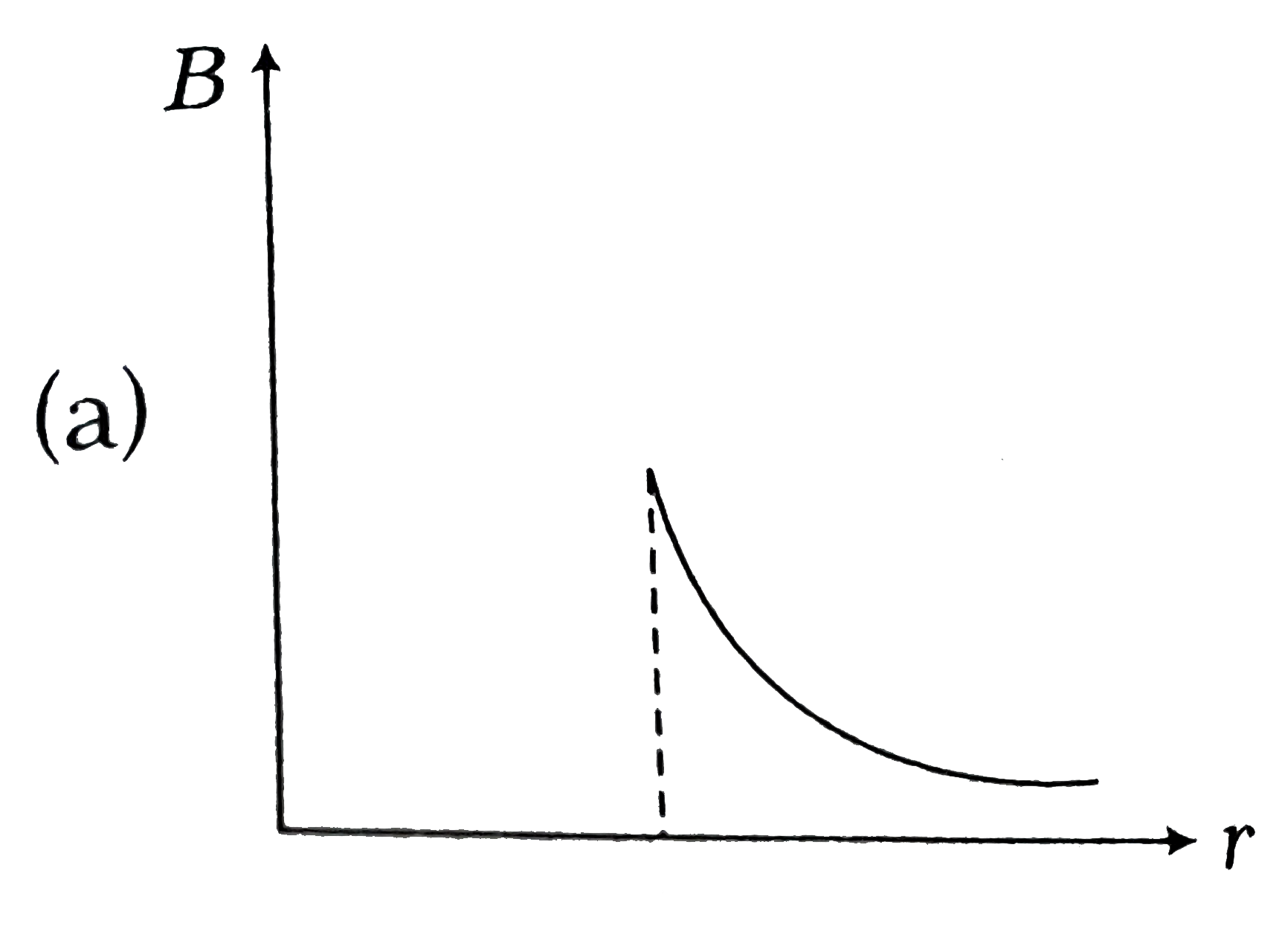
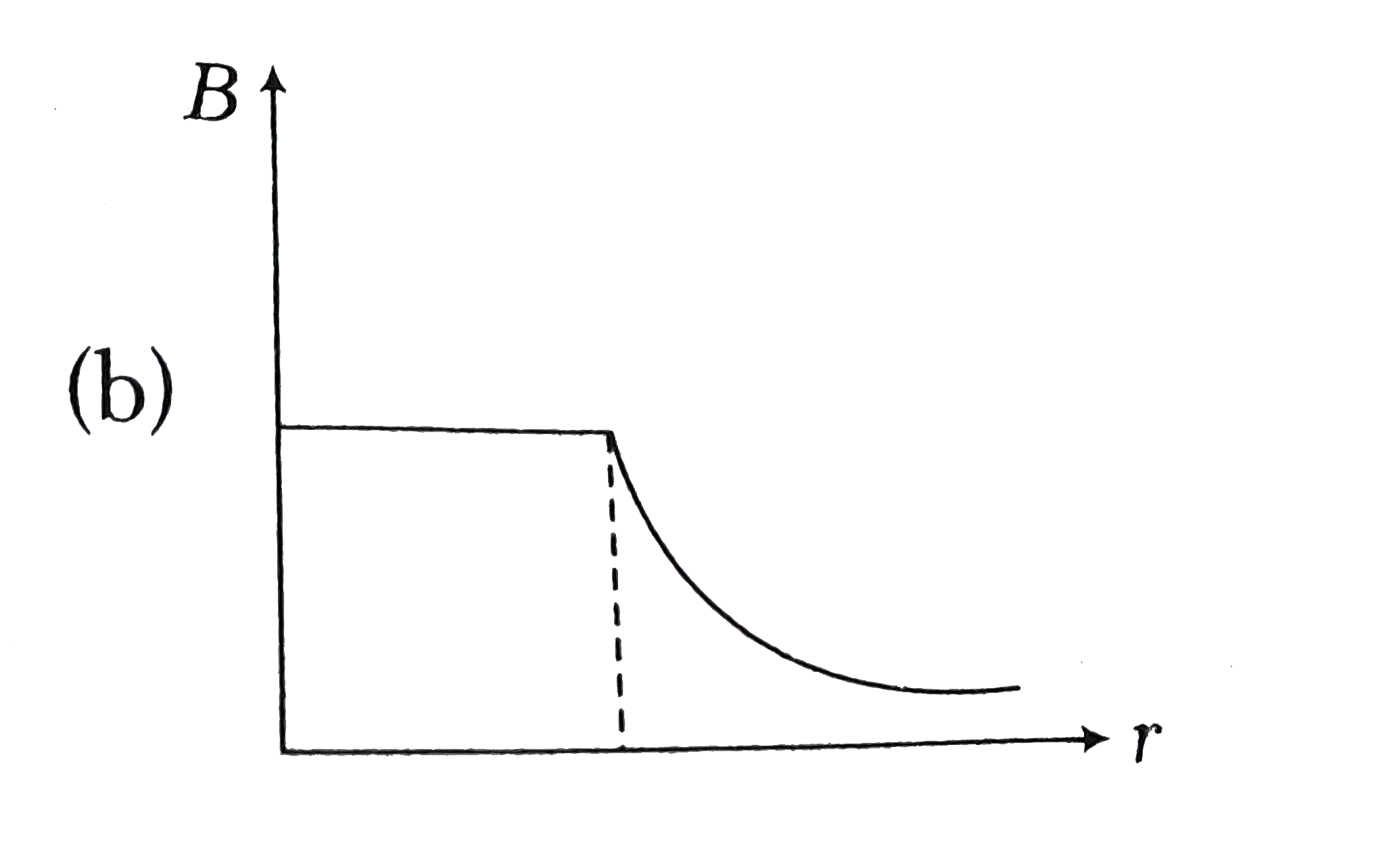
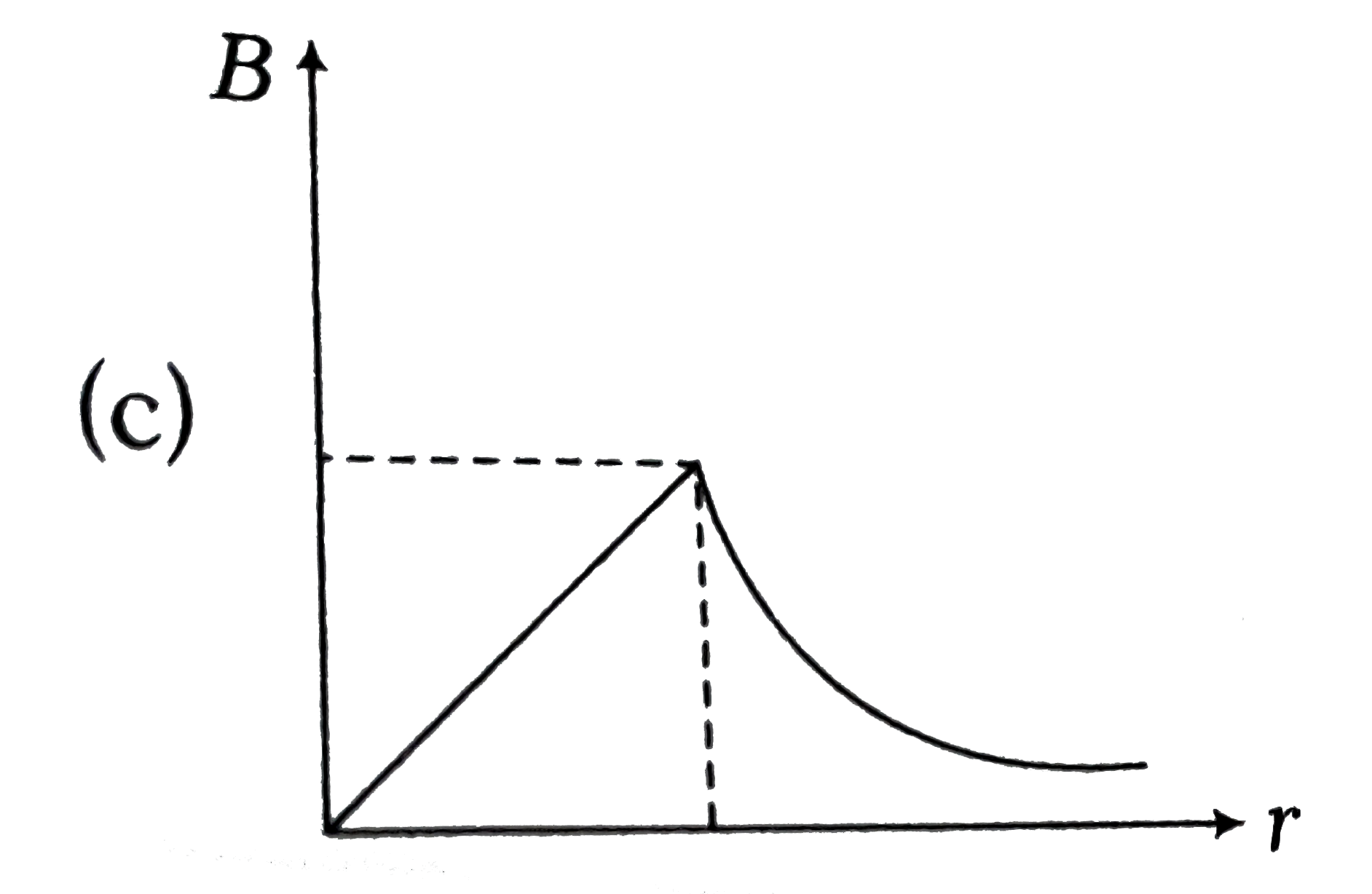
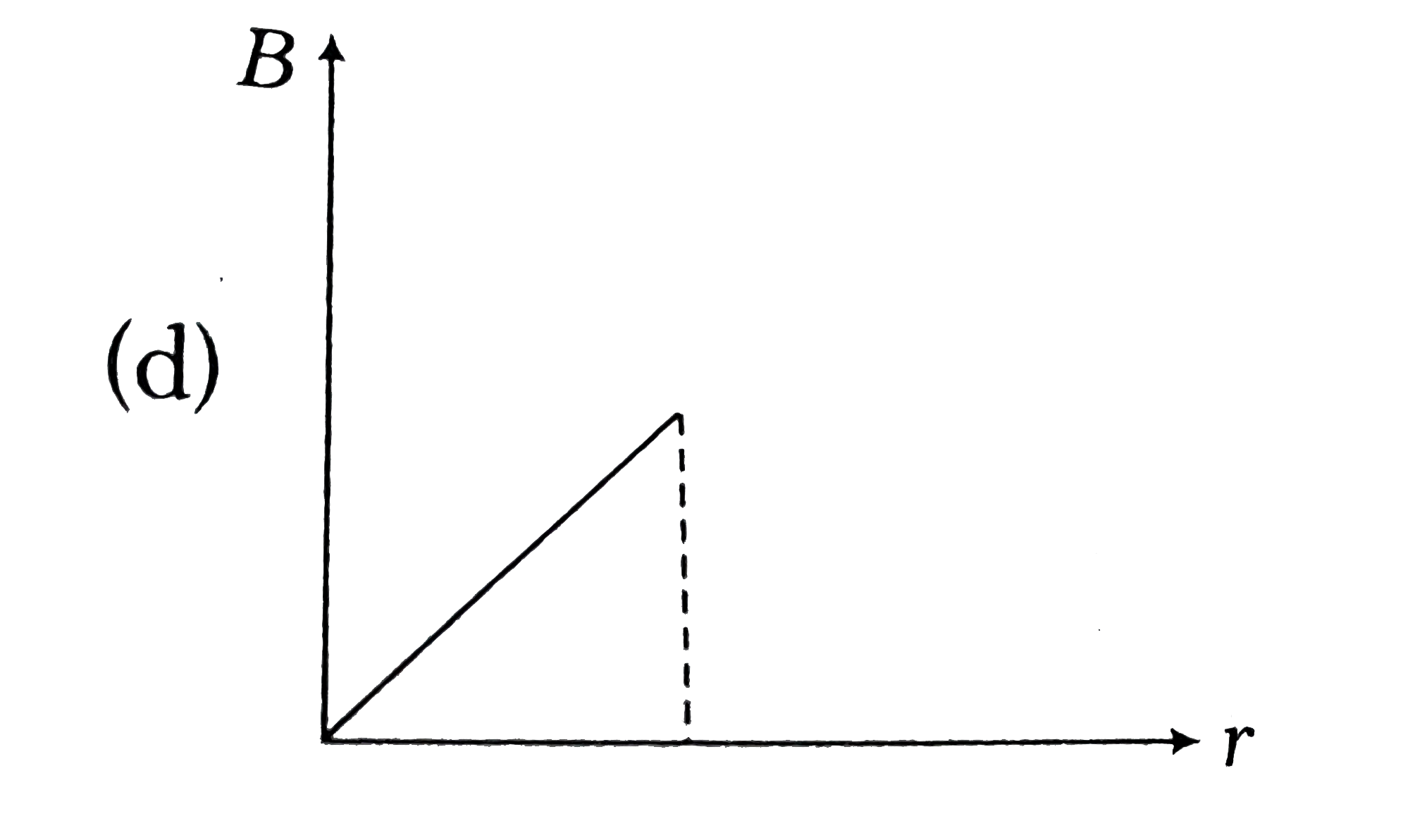
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
MAGNETIC FIELD AND FORCES
DC PANDEY ENGLISH|Exercise Assertion and reason|20 VideosView PlaylistMAGNETIC FIELD AND FORCES
DC PANDEY ENGLISH|Exercise Match the following|4 VideosView PlaylistMAGNETIC FIELD AND FORCES
DC PANDEY ENGLISH|Exercise Check point|54 VideosView PlaylistINTERFERENCE AND DIFFRACTION OF LIGHT
DC PANDEY ENGLISH|Exercise Level 2 Subjective|5 VideosView PlaylistMAGNETICS
DC PANDEY ENGLISH|Exercise MCQ_TYPE|1 VideosView Playlist
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-MAGNETIC FIELD AND FORCES-Taking it together
- A particle of charge q and mass m moves in a circular orbit of radius ...
03:50
|
Play - The maximum energy of a deuteron coming out a cyclotron is 20 MeV. The...
03:34
|
Play - A long thin hollow metallic cylinder of radius 'R' has a current i amp...
02:11
|
Playing Now - In hydrogen atom, an electron is revolving in the orbit of radius 0.53...
04:06
|
Play - A particle of charge q and velocity v passes undeflected through a spa...
05:19
|
Play - The magnetic field at the centre of a circular coil of radius r carryi...
01:25
|
Play - Three long straight wires A, B and C are carrying current as shown in ...
03:46
|
Play - A wire of length 2 m carrying a current of 1 A is bend to form a circl...
03:06
|
Play - A current carrying conductor of length l is bent into two loops one by...
03:06
|
Play - Two charged particles traverse identical helical paths in a completely...
06:11
|
Play - When a certain length of wire is turned into one circular loop, the ma...
01:24
|
Play - A long solenoid carrying a current I is placed with its axis vertical ...
01:42
|
Play - A proton moves at a speed v = 2xx10^(6) m//s in a region of constant m...
03:01
|
Play - An electric current I enters and leaves a uniform circular wire of rad...
01:50
|
Play - A particle of mass m and charge q moves with a constant velocity v alo...
02:28
|
Play - A proton of mass 1.67xx10^(-27) kg charge 1.6xx10^(-19) C is projected...
03:49
|
Play - An equilateral triangle of side length l is formed from a piece of wir...
04:47
|
Play - An infinitely long conductor is bent into a circle as shown in figure....
01:57
|
Play - Magnetic field produced at the point O due to current flowing in an in...
01:58
|
Play - Two identical coils carry equal currents have a common centre and thei...
02:18
|
Play