Recommended Questions
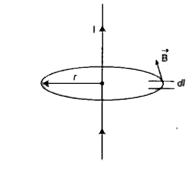
- Using Ampere.s circuital law, obtain an expression for the magnetic fl...
01:39
|
Playing Now - The magnetic flux density at a point distant d from a long straight cu...
01:46
|
Play - Using Ampere's circuital law, obtain an expression for the magnetic in...
02:54
|
Play - Obtain an expression for the magnetic field at a point due to an infin...
02:55
|
Play - State Ampere's circuital law. By using it derive an expression for mag...
03:30
|
Play - Using Ampere.s circuital law derive an expression for magnetic field d...
03:43
|
Play - State Ampere's circuital law . Using it, derive the expression for mag...
05:24
|
Play - Obtain an expression for the magnetic field produced by an infinitely ...
02:56
|
Play - State Ampere's circuital law. By using it derive an expression for mag...
05:57
|
Play