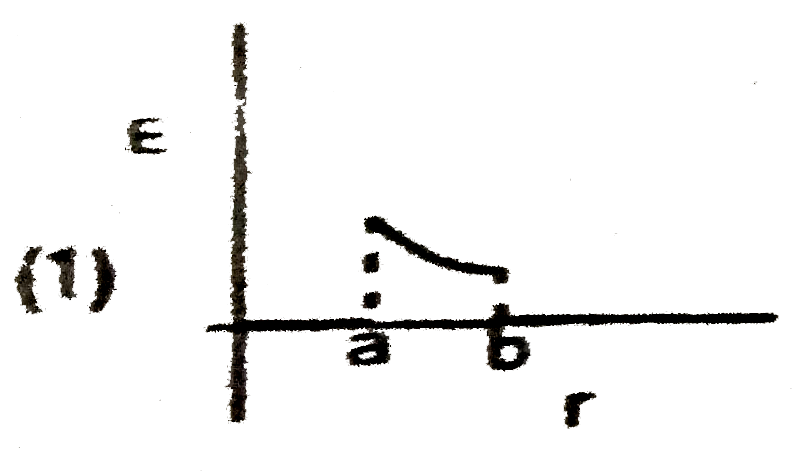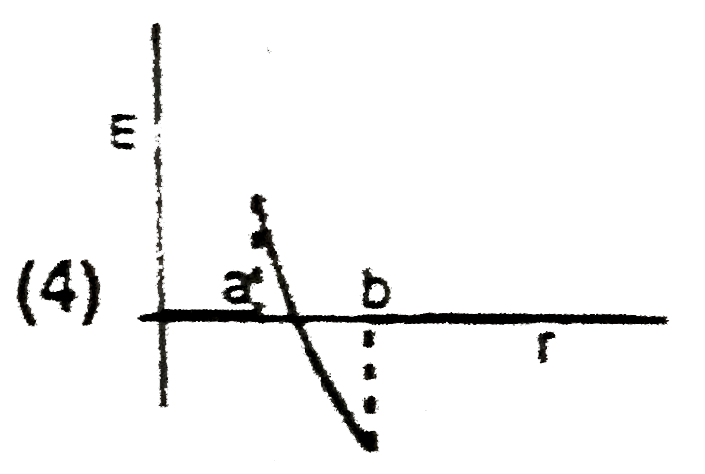Recommended Questions
- For a uniformly charged non conducting sphere of radius R which of fol...
01:21
|
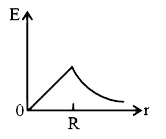
Playing Now - A non-conducting solid sphere of radius R is uniformly charged. The ma...
04:20
|
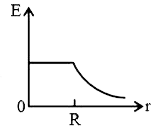
Play - A hallow metal sphere of radius R is uniformly charged. The electric f...
03:28
|
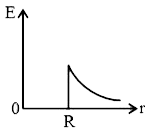
Play - A non-conducting solid sphere of radius R is uniformly charged. The ma...
04:20
|
Play - A non conducting solid sphere of radius R is uniformly charged. The ma...
07:30
|
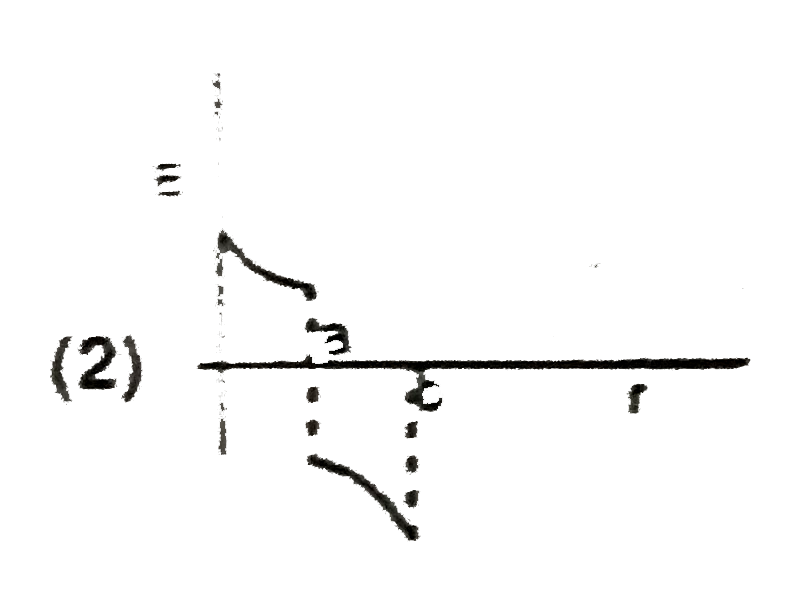
Play - The given graph shows variation (with distance r from centre) of (A)El...
07:15
|
Play - The electric field intensity at a distance 20cm from the centre of a u...
06:50
|
Play - त्रिज्या R के एकसमान आवेशित (कुल आवेश =q ) कुचालक गोले के कारन विधुत क...
03:11
|
Play - An isolated non-conducting solid sphere of radius R is given an electr...
08:35
|
Play