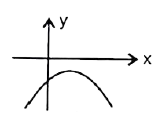
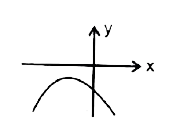
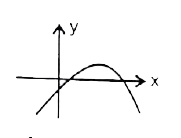
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
QUADRATIC EQUATIONS
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (COMPREHENSION TYPE PROBLEMS)|23 VideosView PlaylistQUADRATIC EQUATIONS
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (MATCHING TYPE PROBLEMS)|4 VideosView PlaylistQUADRATIC EQUATIONS
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (SUBJECTIVE TYPE PROBLEMS)|45 VideosView PlaylistPROBABILITY
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise Exercise -5 : Subjective Type problems|11 VideosView PlaylistSEQUENCE AND SERIES
VIKAS GUPTA (BLACK BOOK) ENGLISH|Exercise EXERCISE (SUBJECTIVE TYPE PROBLEMS)|21 VideosView Playlist
Similar Questions
Explore conceptually related problems
VIKAS GUPTA (BLACK BOOK) ENGLISH-QUADRATIC EQUATIONS -EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
- Let f (x) =x ^(2) -4x +c AA x in R, where c is a real constant, then w...
05:44
|
Play - If 0 lt a lt b lt c and the roots alpha,beta of the equation ax^2 +...
02:30
|
Play - If x satisfies |x-1| + |x-2|+|x-3|gt6, then : i)x ∈ (−∞,1) ii)x ∈...
02:16
|
Play - If both roots of the quadratic equation ax ^(2)+x+b-a =0 are non real ...
05:53
|
Play - If a,b are two numbers such that a ^(2) +b^(2) =7 and a ^(3) + b^(3) =...
09:39
|
Play - The number of non-negative integral ordered pair(s) (x,y) for which (x...
02:35
|
Play - If alpha, beta, gamma and delta are the roots of the equation x ^(4) -...
04:28
|
Play - The value of 'k' for which roots of the equation 4x^2-2x+k=0 are comp...
02:47
|
Play - If a,b,c in R, then for which of the following graphs of the quadrati...
03:44
|
Playing Now - If the equation ax^(2) + bx + c = 0, a,b, c, in R have non -real ro...
05:00
|
Play - If alpha and beta are the roots of the equation ax ^(2) + bx + c=0,a,b...
06:14
|
Play - The equation cos ^(2) x - sin x+lamda = 0, x in (0, pi//2) has roots t...
04:22
|
Play - If the equation ln (x^(2) +5x ) -ln (x+a +3)=0 has exactly one solutio...
02:18
|
Play - The number of non-negative integral ordered pair(s) (x,y) for which (x...
02:35
|
Play - If a lt 0, then the value of x satisfying x ^(2)-2a|x-a| -3a ^(2)=0 i...
10:11
|
Play - If 0 lt a lt b lt c and the roots alpha,beta of the equation ax^2 +...
02:30
|
Play - Solve : | x - 1| + |x - 2| + | x - 3 | gt 6
02:03
|
Play - The value of 'k' for which roots of the equation 4x^2-2x+k=0 are comp...
02:47
|
Play - Let alpha , beta, gamma, delta are roots of x ^(4) -12x ^(3) +lamda x ...
12:14
|
Play - If the points ((a^3)/((a-1))),(((a^2-3))/((a-1))),((b^3)/(b-1)),(((b^2...
04:23
|
Play