Home
Class 11
PHYSICS
A smooth ring of mass m and radius R = 1...

A smooth ring of mass `m` and radius `R = 1 m` is pulled at `P` with a constant acceleration `a= 4 ms^(-2)` on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in `rad//s^(2)`)

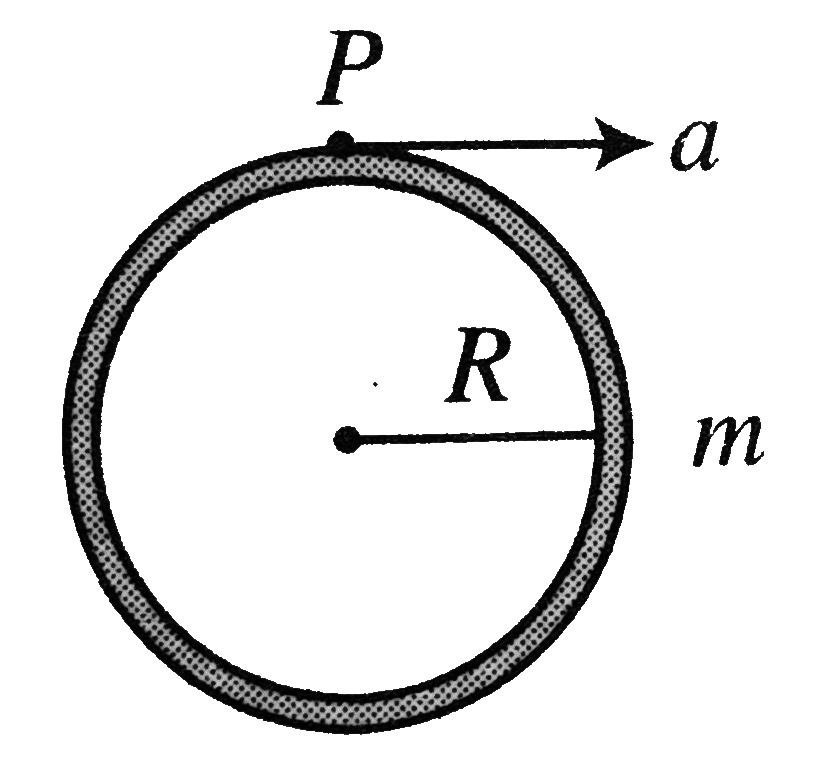
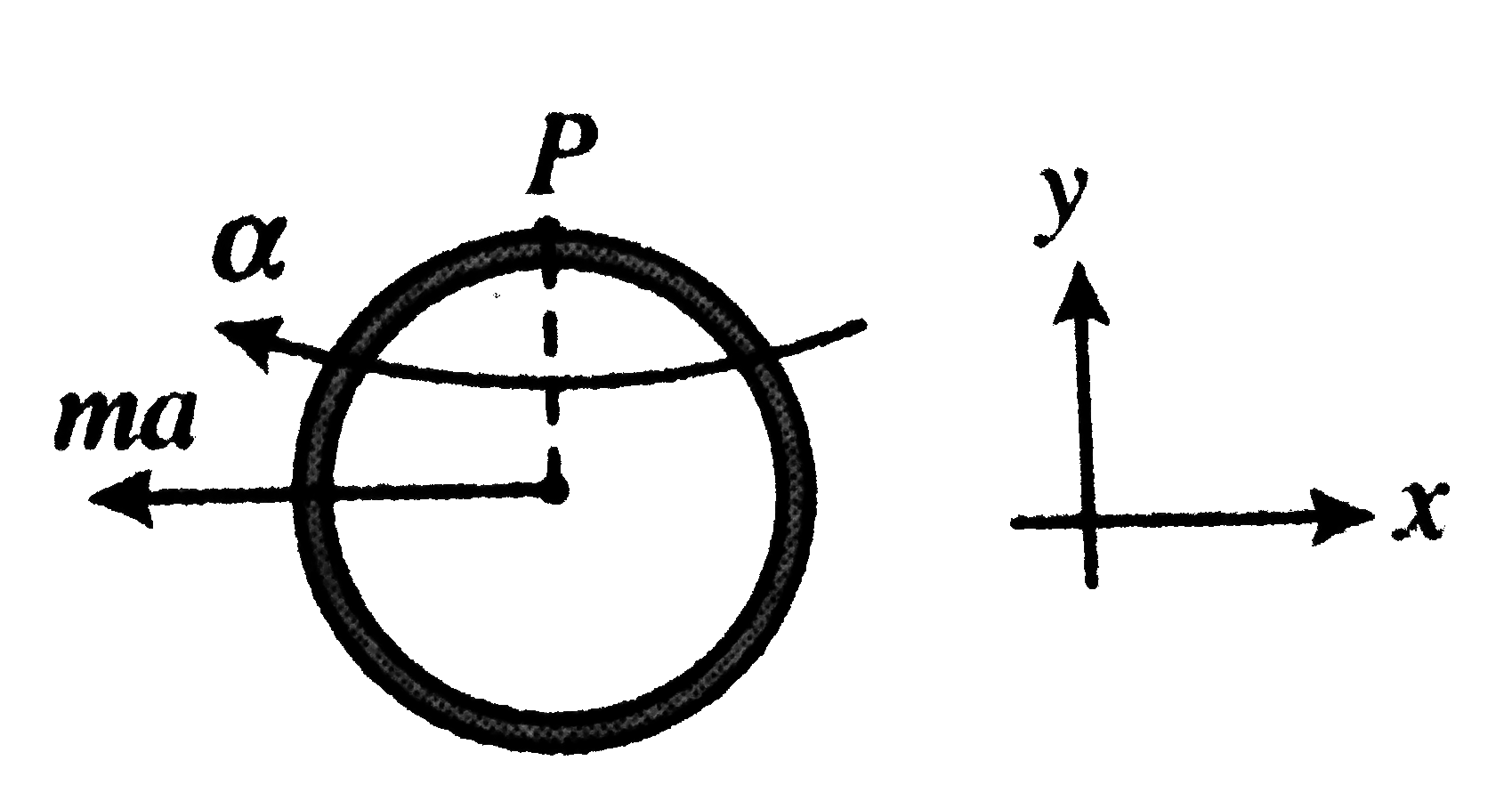
Text Solution

Verified by Experts

The correct Answer is:
2
The pseudo force acting at the `CM` of the ring `vecF_(ps)=-mahati` which produces a torque about `P` given as
`tau_(ps)=-(ma)(R)hatk`

This produce an angular acceleration
`vecalpha=vectau_(ps)/(I_(P))=(-maRhatk)/(2mR^(2))` (`:' I_(P)=mR^(2)+mR^(2)=2mR^(2))`
` =-a/(2R)hatk=4/(2xx1)=2rad//s^(2)`
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS ENGLISH|Exercise Fill In The Blanks|7 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS ENGLISH|Exercise True/False|4 Videos

  • RIGID BODY DYNAMICS 2

    CENGAGE PHYSICS ENGLISH|Exercise Linked Comprehension|71 Videos

  • RIGID BODY DYNAMICS 1

    CENGAGE PHYSICS ENGLISH|Exercise Integer|11 Videos

  • SOUND WAVES AND DOPPLER EFFECT

    CENGAGE PHYSICS ENGLISH|Exercise Integer|16 Videos

Similar Questions

Explore conceptually related problems

A metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.

A non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t^(3)T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be (k)/(24) . Then the value of k is

A non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B = B_0t^2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre. (a) Find friction coefficient mu between the ring and the surface. (b) If magnetic field is switched off after 4 s , then find the angle rotated by the ring before coming to stop after switching off the magnetic field.

A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.

A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If omega is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound is

A conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A . A horizontal magnetic field B=10 T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be .

A conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A . A horizontal magnetic field B=10 T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be .

A sphere of mass m and radius r is placed on a rough plank of mass M . The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v_0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is

In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

Home
Profile