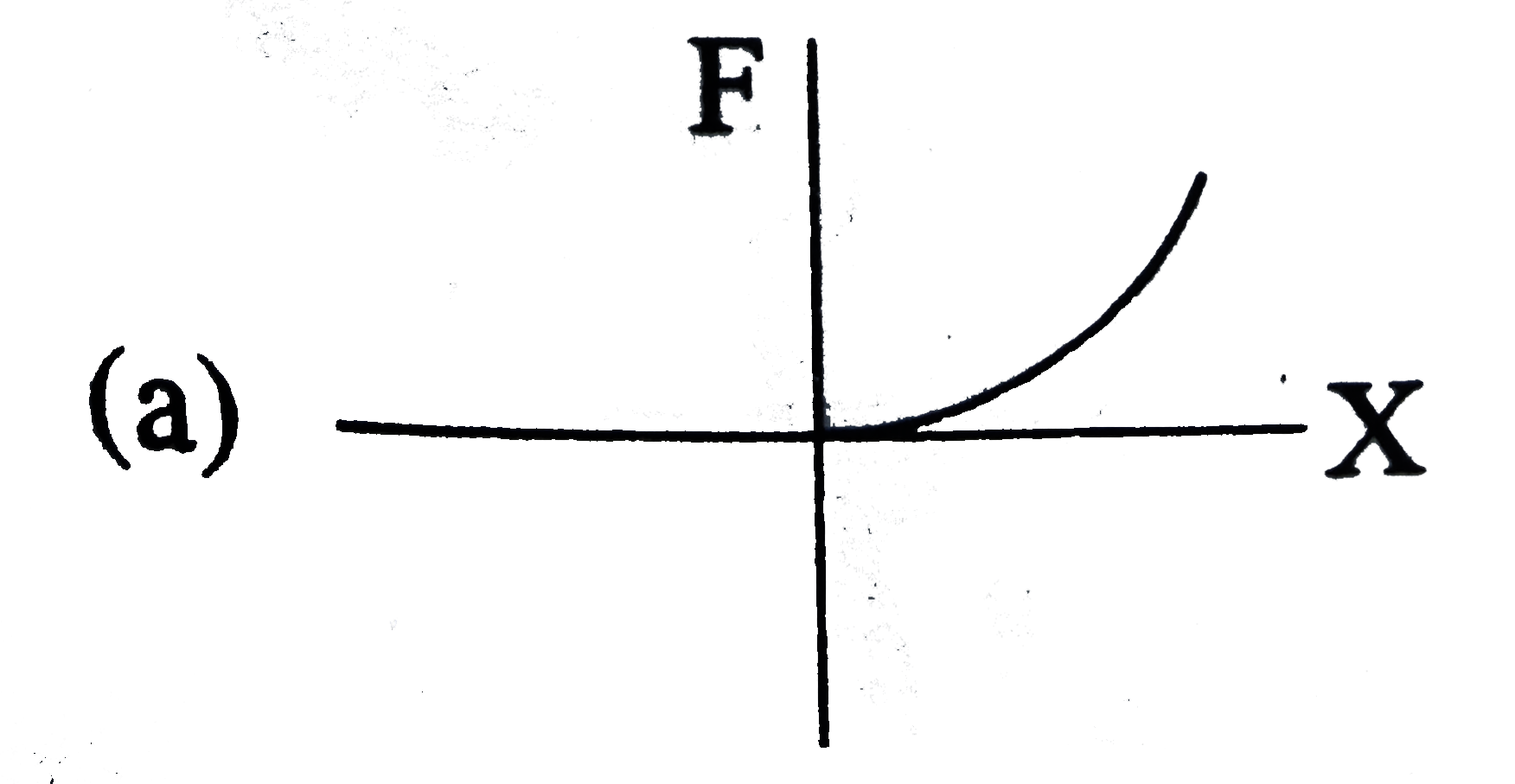
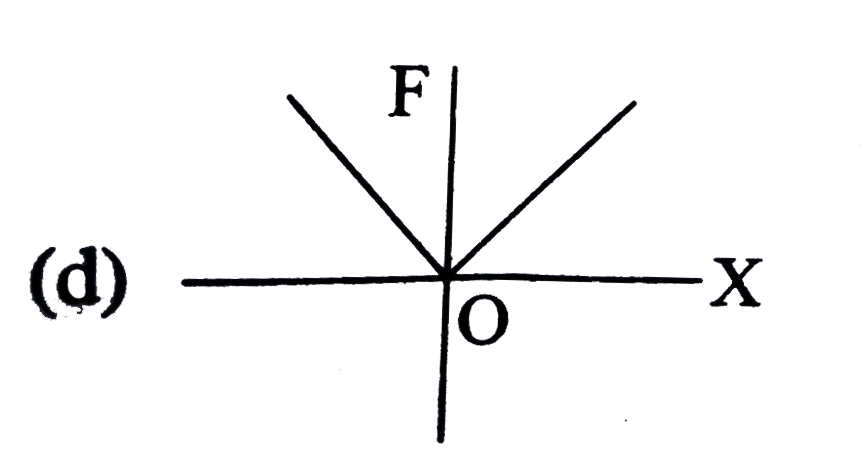
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
|
Topper's Solved these Questions
CENGAGE PHYSICS DPP
CENGAGE PHYSICS ENGLISH|Exercise subjective type|51 VideosView PlaylistCENGAGE PHYSICS DPP
CENGAGE PHYSICS ENGLISH|Exercise Multiple correct Answer Type|54 VideosView PlaylistCAPACITOR AND CAPACITANCE
CENGAGE PHYSICS ENGLISH|Exercise Integer|5 VideosView PlaylistCOULOMB LAW AND ELECTRIC FIELD
CENGAGE PHYSICS ENGLISH|Exercise Single Answer Correct Type|22 VideosView Playlist
Similar Questions
Explore conceptually related problems
Knowledge Check
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-CENGAGE PHYSICS DPP-Single Correct Answer type
- cos(30^circ) is equal to
02:32
|
Play - If sintheta=(1)/(3), then costheta will be
00:56
|
Play - The spring force is given by F=-kx, here k is a constant and x is the ...
00:59
|
Playing Now - A body is attached to a spring whose other end is fixed. If the spring...
01:23
|
Play - A particle starts moving with constant, velocity v=2(m)/(s), from posi...
02:06
|
Play - A stone is allowed to fall freely from a certain Height. Neglecting ai...
03:03
|
Play - If y=x^2+2x-3,y-x graph is
02:12
|
Play - The velcocity displacement graph of a particle moving along a straight...
03:27
|
Play - Which of the following best represents the graph of velocity (v) versu...
02:20
|
Play - Differentiation of sin(x^2) w.r.t. x is
01:16
|
Play - If y=2sin^2theta+tantheta then (dy)/(dtheta) will be
01:37
|
Play - If y=sinx and x=3t then (dy)/(dt) will be
02:01
|
Play - If y=sin(t^2), then (d^2y)/(dt^2) will be
02:39
|
Play - The displace ment of a body at any time t after starting is given by s...
02:13
|
Play - if y=x^2sinx+(3x)/(tanx), then (dy)/(dx) will be
04:10
|
Play - The value of the function (x-1)(x-2)^2 at its maxima is
04:40
|
Play - The adjacent sides of a rectangle with given perimeter as 100 cm and e...
03:26
|
Play - The area of a rectangle will be maximum for the given perimeter, when ...
03:26
|
Play - if x+y=10, thent he maximum value of xy is
03:04
|
Play - the sum of two numbers is fixed. Then its multiplication is maximum, w...
03:05
|
Play