Recommended Questions
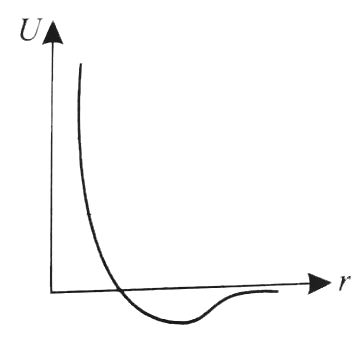
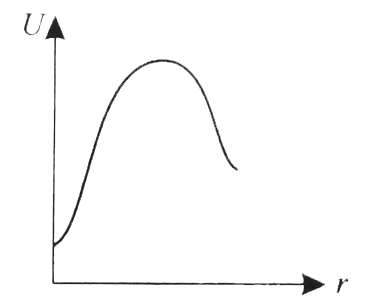
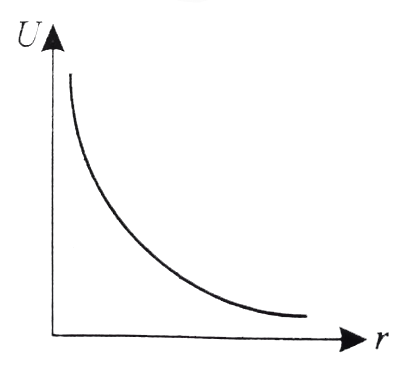
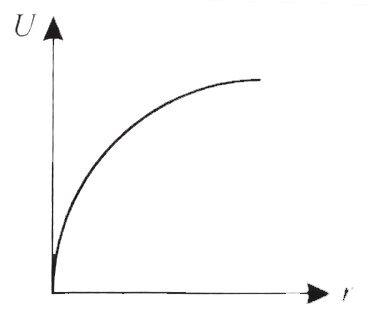
- These diagrams represent the potential energy U of a diatomic molecule...
01:58
|
Playing Now - The potential energy function for a diatomic molecule is U(x) =(a)/(x^...
02:12
|
Play - The potential energy U of diatomic molecules as a function of separati...
03:56
|
Play - The potential energy function for the force between two atoms in a dia...
02:54
|
Play - These diagrams represent the potential energy U of a diatomic molecule...
02:25
|
Play - the points of maximum and minimum attraction in the curve between pote...
04:20
|
Play - The potential energy function for the force between two atoms in a dia...
01:48
|
Play - The potential energy function for the force between two atoms in a dia...
Text Solution
|
Play - एक द्विपरमानुक अणु में दो परमाणुओं के बीच लग रहे बल के लिए स्थितिज ऊ...
07:11
|
Play