Draw a square and construct all its axes of symmetry. Measure the angles between each pair of succesive axes of symmetry. What do you notice? Does the same rule apply for other regular polygon?
Draw a square and construct all its axes of symmetry. Measure the angles between each pair of succesive axes of symmetry. What do you notice? Does the same rule apply for other regular polygon?
Answer
Step by step text solution for Draw a square and construct all its axes of symmetry. Measure the angles between each pair of succesive axes of symmetry. What do you notice? Does the same rule apply for other regular polygon? by MATHS experts to help you in doubts & scoring excellent marks in Class 7 exams.
|
Topper's Solved these Questions
SYMMETRY
NCERT TELUGU|Exercise Try this|14 VideosView PlaylistSYMMETRY
NCERT TELUGU|Exercise Do this |6 VideosView PlaylistSUMMATIVE ASSESMENT -II
NCERT TELUGU|Exercise EXERCISE|30 VideosView PlaylistTRIANGLE AND ITS PROPERTIES
NCERT TELUGU|Exercise EXERCISE - 1|4 VideosView Playlist
Similar Questions
Explore conceptually related problems
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one as symetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the as symmetric carbon. In fact, they represent as symetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its mirror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Which of the following statements is correct regarding compounds I to III
Watch solution
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one as symetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the as symmetric carbon. In fact, they represent as symetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its mirror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Consider the following structures A,B,C,D Which of the following statements is not correct
Watch solution
Knowledge Check
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one assymetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the assymmetric carbon. In fact, they represent assymetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its miror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Which of the following compounds is optically inactive
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one assymetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the assymmetric carbon. In fact, they represent assymetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its miror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Which of the following compounds is optically inactive
A

B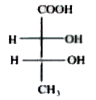

C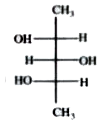

D

Submit
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one as symetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the as symmetric carbon. In fact, they represent as symetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its mirror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Which of the following compounds is optically inactive
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one as symetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the as symmetric carbon. In fact, they represent as symetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its mirror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Which of the following compounds is optically inactive
A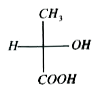
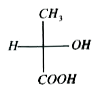
B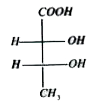

C

D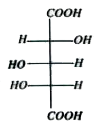

Submit
An organic compound having a carbon attached to four different groups is optically active. But is it that opposite is also true? That is, do all optically active organic compounds have chiral carbons? Not necessarily. Presence or absence of chiral centre is not the sufficient criteria for optical activity. The ultimate criteria is presence or absence of either plane or centre of symmetry. Two compounds which are non superimposable mirror images of each other are called enantiomers. If a compound contains more than one chiral carbon, new words are required to describe the relationship between various stereisomers of the compound. Those words are diastereomers and mesomers. Optically active compounds among the following is
An organic compound having a carbon attached to four different groups is optically active. But is it that opposite is also true? That is, do all optically active organic compounds have chiral carbons? Not necessarily. Presence or absence of chiral centre is not the sufficient criteria for optical activity. The ultimate criteria is presence or absence of either plane or centre of symmetry. Two compounds which are non superimposable mirror images of each other are called enantiomers. If a compound contains more than one chiral carbon, new words are required to describe the relationship between various stereisomers of the compound. Those words are diastereomers and mesomers. Optically active compounds among the following is
A
`CH_3 CH_2 undersetoverset(|)(Cl)(C )HCH_2CH_3`
B
`CH_3CH_2 undersetoverset(|)(Cl)( C) DCH_2CH_2`
C
`CH_3CH_2CHDCH_2CH_3`
D
`CH_3CH_2CHDCH_3`
Submit
Similar Questions
Explore conceptually related problems
The necessary condition for a molecule to exhibit optical isomerism is dissymmetry or chiral. Thus all organic compounds which contain one assymetric carbon atom are chiral and exist in two stereoisomers. Although the two forms have the same structure, they have different arrangements of groups about the assymmetric carbon. In fact, they represent assymetric molecules. They do not have a plane of symmetry. They are related to each other as an object to its miror image and are non superimposable. The two structures actually stand for dextro or (+) and leavo or (-) isomers. Since they are related each other as mirror images, they are commonly called enantiomers. Consider the following structers A,B,C,D Which of the following statements is not correctConsider the following structers A,B,C,D Which of the following statements is not correct
Watch solution
Draw two lines on a paper as shown below. Do they intersect each other? Can you call them parallel lines? Give reason. Make a pair of parallel lines what is the angle formed between them ? Think, discuss with your friends and teacher.
Watch solution
Structural isomers have different covalent linkage of atoms. Stereoisomers are compounds that have same sequence of covalent bonds but differ in the relative dispositions of their atoms in space. Geometrical and optical isomers are the two important types of configurational isomers. The compound with double bonds or ring structure have restricted rotation, so exist in two geometrical forms. The double bonds in larger rings (ring size 10 carbon large) can also cause geometrical isomerism. The optical isomers rotate the plane of plane-polarised light. A sp^3 -hybridised carbon atom bearing four different types of substituents is called an asymmetric centre or chiral centre. A chiral object or molecule cannot be superimposed on its mirror image. Stereoisomers that are mirror images of each other are called enantiomers. The stereosomers that the pot mirror images of each other are called diastereomers. Diasteremers have different physical properties. A racemic mixture is optically inactive and contains equal amounts of both the enantiomers. Resolution refers to method of separating a racemic mixture. Into two pure enantiomers. A meso compound is an optically inactive stereoisomer, which is achiral due to the presence of an internal plane of symmetry or centre of symmetry within the molecule. The pair of showing identical species is
Watch solution
Structural isomers have different covalent linkage of atoms. Stereoisomers are compounds that have same sequence of covalent bonds but differ in the relative dispositions of their atoms in space. Geometri cal and optical isomers are the two important types of configurational isomers. The compound with double bonds or ring structure have restricted rotation, so exist in two geometrical forms. The double bonds in larger rings (ring size 10 carbon large) can also cause geometrical isomerism. The optical isomers rotate the plane of plane-polarised light. A sp^(3) -hybridised carbon atom bearing four different types of substituents is called an asymmetric centre or chiral centre. A chiral object or molecule cannot be superimposed on its mirror image. Stereoisomers that are mirror images of each other are called enantiomers. The stereosomers that the pot mirror images of each other are called diastereomers. Diasteremers have different physical properties. A racemic mixture is optically inactive and contains equal amounts of both the enantiomers. Resolution refers to method of separating a racemic mixture. Into two pure enantiomers. A meso compound is an optically inactive stereoisomer, which is achiral due to the presence of an internal plane of symmetry or centre of symmetry within the molecule. The pair of showing identical species is
Watch solution
An orbital is designated by certain values of first three quantum numbers (n, l and m) and according to Pauli.s exclusion principle, no two electrons in a atom can have all the for quantum numbers equal. N, l and m denote size, shape and orientation of the orbital. The permissible values of n are 1,2,3.... prop while that of 1 are all possible integral values from 0 to n-n. Orbitals with same values of n and 1 but different values of m (where m can have any integral values from 1 to +1 including zero) are of equal energy and are called degenerate orbitals. However degeneracy is destroyed in homogeneous external magnetic field due to different extent of interaction between the applied field and internal electronic magnet of different orbitals differing in orientations. In octahedral magnetic field external magnetic field as oriented along axes while in tetrahedral field the applied field actas more in between the axes than that on the axes themselves. For 1=0, 1,2,3,...., the states (called sub-shells) are denoted by the symbol s,p,d,f.....respectively. After f, the subshells are denoted by letters alphabetically 1 determines orbital angular motion (L) of electron as L = sqrt(l(l+1))(h)/(2pi) ON the other hand, m determines Z-component of orbital angular momentum as L_(Z) = m((h)/(2pi)) Hund.s rule states that in degenerate orbitals electrons do not pair up unless and until each each orbitals has got an electron with parallesl spins Besides orbital motion,an electron also posses spin-motion. Spin may be clockwise and anticloskwise. Both these spin motions are called two spins states of electrons characterized by spin Q.N (s) : s = +(1)/(2) and = -(1)/(2) respectively The sum of spin Q.N. of all the electrons is called total spin(s) and 2s+1 is called spin multiplicity of the configuration as a whole. The spin angular momentum of an electron is written as L_(s) = sqrt(s(s+1))(h)/(2pi) According to Hund.s rule, the distribution of electron within the various orbitals of a given sub-shell is one which is associated with
Watch solution
NCERT TELUGU-SYMMETRY-Exercise - 2 (true or false)
- Draw a square and construct all its axes of symmetry. Measure the angl...
06:02
|
Playing Now - (True/false) Every closed figure has an axis of symmetry
02:44
|
Play - (True/false)A figure with atleast one axis of symmetry is called a sym...
02:44
|
Play - (True/false) A regular polygon of 10 sides will have 12 axes of symmet...
04:18
|
Play